Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 4
A Convenient Synthesis of Trisubstituted 1,3,5-triazine Derivatives and their Antimicrobial Screening
Archana Y Cholera* and Kartik D Ladva
Department of Chemistry, Shree M. & N. Virani Science College, Rajkot-360005, Gujarat, India
- *Corresponding Author:
- Archana Y Cholera
Department of Chemistry
Shree M. & N. Virani Science College
Rajkot-360005, Gujarat, India
Abstract
A series of novel 1,3,5-triazine derivatives bearing various aryl amine, 2-amino pyrazine and 4-hydroxy coumarin moieties as substituents have been synthesized by an easy and conventional method using sequential nucleophilic substitution of chlorine atoms of cyanuric chloride. The reaction of cyanuric chloride with 4-hydroxy coumarin in acetone using alkaline medium at 0-5°C was afforded compound 3 in good yield. Followed by reaction 3 with 2-amino pyrazine and then various aromatic amines have afforded target compounds 6a-n in good yields. All the newly synthesized compounds were characterized by using spectroscopic analysis and then examined for their ability to inhibit the two Gram-positive bacteria (Bacillus subtilis and Staphylococcus aureus) Gram-negative bacteria (Escherichia coli and Pseudomonas aeruginosa) and one fungal species (Aspergillus niger) for biological interest.
Keywords
1,3,5-Triazine, 4-Hydroxy coumarin, 2-Amino pyrazine, Trisubstituted triazines
Introduction
Coumarin derivatives have played a pivotal role in medicinal chemistry due their broad biological properties [1]. Among the various coumarin derivatives, 4-hydroxy coumarins are potential in therapeutic applications such as anticancer [2], antimalarial [3], antifungal [4], antiviral [5], anticoagulants [6]. They have yielded important results as antibiotics (Novobiocin) [7], anti-AIDS agents (Calanolides) [8] and antitumor drugs (Gelparvarin) [9]. Some of these drugs derived from 4-hydroxycoumarin have been thoroughly investigated [10]. Pyrazine derivatives possess a broad spectrum of biological activity and fulfill an important function in animal metabolism [11] and also other applications [12,13]. These compounds are also used as spasmolytic drug [14] in several countries, fluorescent brightener, efficient laser dye, standard for fluorometric determination of enzymatic activity, as a starting material for the preparation of insecticide [15], as precursor for furano coumarins and many other derivatives of substituted coumarins and analytical reagents [16].
Nitrogen containing heterocyclic compounds plays a significant role in the field of biological and medicinal among them 1,3,5-triazine skeleton is more interesting structure and has a wide variety of interesting applications in numerous fields [17]. Various derivatives of s-triazine show antimicrobial [18,19], antifungal [20], antitumor [21] and herbicidal [22] activities. Some are also used for the treatment of HIV infection [23]. Several workers investigated the s-triazine nucleus in the scope of potential therapeutic agents for diseases due to bacteria, malaria and cancer [24]. The above literature survey led us to consider the s-triazine nucleus as a core scaffold. It has been reported that s-triazine derivatives are used as templates for molecular imprinting [25] and for the construction of three-helix bundle protein [26].
It has been extensively reported that the presence of 4-hydroxy coumarin and pyrazine moieties in 1,3,5-triazine may enhance their biological activity [27-31]. Thus keeping in mind the tremendous biological potential of cyanuric chloride, 4-hydroxy coumarin and pyrazine derivatives motivated us to develop an easy and clean route for construction of novel triazine derivatives and examined their biological activity.
Material and Methods
All melting points were recorded using open capillary and are uncorrected. 1H-NMR spectra were obtained using a Bruker model spectrophotometer and were recorded at 400 MHz in Deuterated Dimethyl Sulfoxide (DMSO-d6). Chemical shifts are reported in ppm relative to the residual signal of the solvent. IR spectra were recorded on a FTIR-Schimadzu. Mass spectrums were recorded using GCMS-Agilent. Chemicals and solvents were purchased from Loba Chemi, Himedia, Sigma-Aldrich and used without purification.
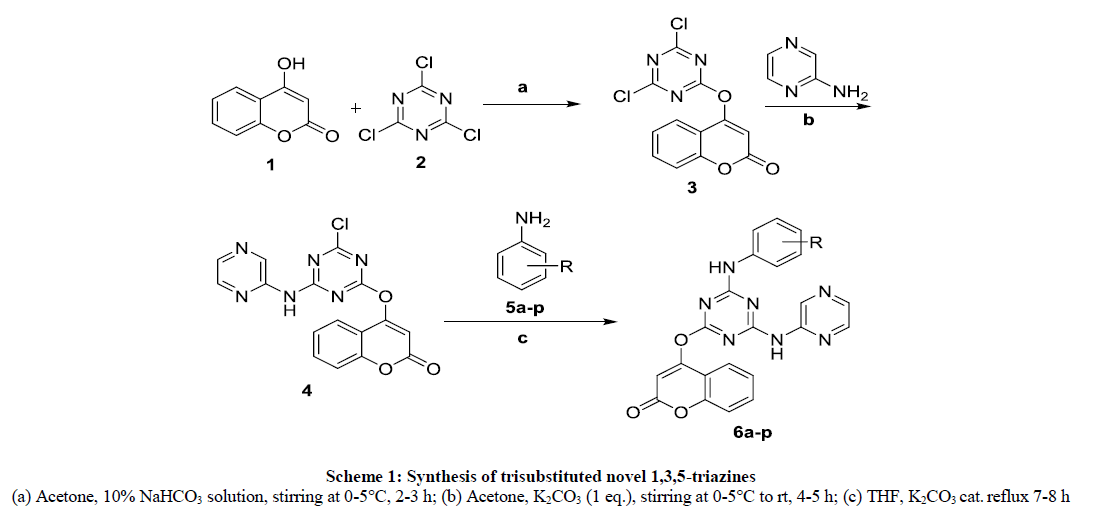
Synthesis of 2-(Coumarinyl-4-oxy)-4,6-dichloro-s-triazine (3)
To a stirred solution of cyanuric chloride (0.05 mol, 9.2 g) in acetone (50 ml) at 0-5°C, the solution of 4-hydroxy coumarin (0.05 mol, 8.1 g) in 10% NaHCO3 (45 ml) was added drop wise in two hours. The reaction was being monitored by TLC using acetone: toluene (10:1) as eluent. After completion of reaction, the stirring was stopped and the reaction mixture was poured in to crushed ice. The product obtained was filtered and dried. The crude product was purified by recrystallization from acetone to give the title compound (3); yield 87%, M.p. 208-210°C.
Synthesis of 4-((4-chloro-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one (4)
To a stirred solution of compound 3 (1 g, 3.2 mmol) in acetone 20 ml was added K2CO3 (0.5 g, 3.2 mmol) at 0-5°C for 10 min. The solution of 2-amino pyrazine (306 mg, 3.2 mmol) in acetone 5 ml was added to above reaction mixture slowly drop wise during time period of 15 min. after completion of addition, the reaction was stirred at room temperature for 5 to 6 h. The reaction was being monitored by TLC using Toluene: Acetone (1:5) Rf: 0.21. After completion of the reaction, the reaction was poured in to crushed ice to yield the desired product. The product was filtered off and air dried to use further without purification. Yield 78%, mp 220-222°C.
General synthesis of 4-((4-(arylamino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one 6a-n
The mixture of 4-((4-chloro-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one (500 mg, 1.39 mmol), various aryl amines (1.3 mmol), catalytic amount of K2CO3 and THF was heated under reflux condition for 7-8 h. After completion of the reaction, it was poured in to crushed ice. The separated product was filtered, dried and crystallized out from chloroform to yield the desired products 6a-n.
Physical and spectral data of 4-((4-chloro-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: White color solid; Rf: 0.28; IR (KBr cm-1): 3452, 2812, 2778, 1742, 1524, 1429, 1320, 856, 755; 1H-NMR (400 MHz, DMSO-d6); δ ppm 5.65 (s, 1H) 7.03-7.77 (m, ArH), 7.86 (1H, NH); Mass (m/z): 309 [m+1]; Anal. Calcd. for C12H5Cl2N3O3. Calculated C: 46.48, H: 1.63, N: 13.55. Found C: 46.45, H: 1.60, N: 13.52.
Physical and spectral data of compounds 6a-n
4-((4-(phenylamino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Cream solid; Rf: 0.21; IR (KBr cm-1): 3452, 3448, 2762, 2745, 1752, 1624, 1520, 1409, 1314, 875, 775; 1H-NMR (400 MHz, DMSO-d6); δ ppm 5.99 (s, 1H), 7.19-7.77 (m, 11H), 8.84 (s, 1H), 9.94 (s, 1H); Mass (m/z): 425; Anal. Calcd. for C22H15N7O3. Calculated C: 62.11, H: 3.55, N: 23.05. Found C: 62.09, H: 3.51, N: 23.02.
4-((4-((4-methoxyphenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Reddish solid; Rf: 0.22; IR (KBr cm-1): 3452, 3450, 2852, 2735, 1781, 1618, 1534, 1407, 1312, 898, 751; 1H-NMR (400 MHz, DMSO-d6); δ ppm 3.80 (s, 3H), 6.43 (s, 1H), 6.81-8.95 (m, 11H), 8.97 (s, 1H), 9.95 (s, 1H); Mass (m/z): 455; Anal. Calcd. for C23H17N7O4. Calculated C: 60.66, H: 3.76, N: 21.53. Found C: 60.59, H: 3.75, N: 21.52.
4-((4-((3-chlorophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Pista green color solid; Rf: 0.21; IR (KBr cm-1): 3460, 3450, 2822, 2725, 1757, 1632, 1521, 1452, 1310, 874, 721; 1H-NMR (400 MHz, DMSO-d6); δ ppm 6.23 (s, 1H), 6.91-8.25 (m, 11H), 8.56 (s, 1H), 9.95 (s, 1H); Mass (m/z): 460 [m+1]; Anal. Calcd. for C22H14ClN7O3. Calculated C: 57.46, H: 3.07, N: 21.32. Found C: 57.49, H: 3.05, N: 21.30.
4-((4-((4-nitrophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Yellow color solid; Rf: 0.20; IR (KBr cm-1): 3455, 3440, 2822, 2725, 1747, 1622, 1561, 1452, 1444 1320, 874, 721; 1H-NMR (400 MHz, DMSO-d6); δ ppm 6.22 (s, 1H), 7.11-8.24 (m, 11H), 8.32 (s, 1H), 9.94 (s, 1H); Mass (m/z): 470; Anal. Calcd. for C22H14ClN7O3. Calculated C: 56.17, H: 3.00, N: 23.82. Found C: 56.19, H: 3.01, N: 23.80.
4-((4-((4-bromophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Green color solid; Rf: 0.22; IR (KBr cm- 1): 3565, 3540, 2821, 2625, 1717, 1656, 1555, 1474, 1414 1344, 856, 711; 1H-NMR (400 MHz, DMSO-d6); δ ppm 6.24 (s, 1H), 7.01-8.11 (m, 11H), 8.39 (s, 1H), 9.54 (s, 1H); Mass (m/z): 504[m+1]; Anal. Calcd. for C22H14BrN7O3. Calculated C: 52.40, H: 2.80, N: 19.44. Found C: 52.39, H: 2.79, N: 19.40.
4-((4-((4-fluorophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Dark green color solid; Rf: 0.22; IR (KBr cm-1): 3465, 3452, 2751, 2622, 1718, 1626, 1514, 1457, 1321, 851, 721; 1H-NMR (400 MHz, DMSO-d6); δ ppm 5.91 (s, 1H), 7.09-8.14 (m, 11H), 8.41 (s, 1H), 9.44 (s, 1H); Mass (m/z): 444[m+1]; Anal. Calcd. for C22H14FN7O3. Calculated C: 59.59, H: 3.18, N: 22.11. Found C: 59.60, H: 3.18, N: 22.10.
4-((4-((4-chlorophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Green color solid; Rf: 0.22; IR (KBr cm- 1): 3462, 3423, 2885, 2774, 1789, 1632, 1522, 1451, 1310, 875, 770; 1H-NMR (400 MHz, DMSO-d6); δ ppm 6.38 (s, 1H), 7.23-8.23 (m, 11H), 8.37 (s, 1H), 9.97 (s, 1H); Mass (m/z): 460 [m+1]; Anal. Calcd. for C22H14ClN7O3. Calculated C: 57.46, H: 3.07, N: 21.32. Found C: 57.50, H: 3.03, N: 21.31.
4-((4-((3-nitrophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Yellow color solid; Rf: 0.21; IR (KBr cm-1): 3453, 3442, 2831, 2721, 1745, 1632, 1551, 1453, 1445 1322, 874, 767; 1H-NMR (400 MHz, DMSO-d6); δ ppm 6.19 (s, 1H), 7.14-8.21 (m, 11H), 8.39 (s, 1H), 9.84 (s, 1H); Mass (m/z): 470; Anal. Calcd. for C22H14ClN7O3. Calculated C: 56.17, H: 3.00, N: 23.82. Found C: 56.19, H: 3.00, N: 23.82.
4-((4-(pyrazin-2-ylamino)-6-(p-tolylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Yellow solid; Rf: 0.23; IR (KBr cm-1): 3451, 3450, 2772, 2737, 1751, 1621, 1532, 1440, 1378, 1247, 884, 762; 1H-NMR (400 MHz, DMSO-d6); δ ppm 2.32 (s, 3H), 6.21 (s, 1H), 7.01-8.07 (m, 11H), 8.36 (s, 1H), 9.74 (s, 1H); Mass (m/z): 439; Anal. Calcd. for C23H17N7O3. Calculated C: 62.87, H: 3.90, N: 22.31. Found C: 62.89, H: 3.91, N: 22.32.
4-((4-((2-methoxyphenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Reddish solid; Rf: 0.23; IR (KBr cm-1): 3456, 3440, 2832, 2635, 1766, 1647, 1534, 1410, 1339, 874, 735; 1H NMR (400 MHz, DMSO-d6); δ ppm 3.87(s, 3H), 6.37(s, 1H), 6.91-8.23(m, 11H), 8.36 (s, 1H), 9.03 (s, 1H); Mass (m/z): 455; Anal. Calcd. for C23H17N7O4 Calculated C:60.66, H: 3.76, N:21.53. Found C: 60.60, H: 3.74, N: 21.51.
4-((4-(pyrazin-2-ylamino)-6-(o-tolylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Yellow solid; Rf: 0.23; IR (KBr cm-1): 3457, 3450, 2772, 2737, 1756, 1624, 1571, 1451, 1384, 1251, 878, 752; 1H-NMR (400 MHz, DMSO-d6); δ ppm 2.27 (s, 3H), 6.22 (s, 1H), 6.91-8.17 (m, 11H), 8.32 (s, 1H), 9.14 (s, 1H); Mass (m/z): 439; Anal. Calcd. for C23H17N7O3. Calculated C: 62.87, H: 3.90, N: 22.31. Found C: 62.87, H: 3.90, N: 22.30.
4-((4-((2-fluorophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Cream color solid; Rf: 0.23; IR (KBr cm- 1): 3465, 3412, 2751, 2662, 1718, 1657, 1514, 1432, 1321, 871, 745; 1H-NMR (400 MHz, DMSO-d6); δ ppm 6.11 (s, 1H), 7.01-8.11 (m, 11H), 8.38 (s, 1H), 9.24 (s, 1H); Mass (m/z): 444[m+1]; Anal. Calcd. for C22H14FN7O3. Calculated C: 59.59, H: 3.18, N: 22.11. Found C: 59.61, H: 3.18, N: 22.11.
4-((4-((2-chlorophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Green color solid; Rf: 0.23; IR (KBr cm- 1): 3461, 3453, 2827, 2765, 1889, 1745, 1632, 1525, 1451, 1310, 872, 762; 1H-NMR (400 MHz, DMSO-d6); δ ppm 6.33 (s, 1H), 7.21-8.22 (m, 11H), 8.36 (s, 1H), 9.91 (s, 1H); Mass (m/z): 460 [m+1]; Anal. Calcd. for C22H14ClN7O3. Calculated C: 57.46, H: 3.07, N: 21.32. Found C: 57.52, H: 3.05, N: 21.30.
4-((4-((2-bromophenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one: Green color solid; Rf: 0.22; IR (KBr cm- 1): 3515, 3480, 2822, 2615, 1711, 1656, 1573, 1422, 1428 1363, 857, 728; 1H-NMR (400 MHz, DMSO-d6); δ ppm 6.26 (s, 1H), 7.01-8.11 (m, 11H), 8.38 (s, 1H), 9.56 (s, 1H); Mass (m/z): 504[m+1]; Anal. Calcd. for C22H14BrN7O3. Calculated C: 52.40, H: 2.80, N: 19.44. Found C: 52.40, H: 2.80, N: 19.41.
Results and Discussion
The triazine frame of cyanuric chloride can be conveniently manipulated by the sequential displacement of its chlorine atoms by oxygen and nitrogen containing nucleophiles in presence of acid scavenger. It is a temperature controlled and a step wise process. Initially, reaction of cyanuric chloride with 4-hydroxy coumarin was carried out using acetone as solvent at 0-5°C in alkaline medium to yield 4-((4,6-dichloro-1,3,5- triazin-2-yl)oxy)-2H-chromen-2-one. Further, the reaction of compound 3 with 2-amino pyrazine was achieved using acetone as solvent and K2CO3 as base at room temperature. To synthesize desired compounds, the reaction of various aryl amines with 4-((4-chloro-6-(pyrazin-2- ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one was carried using THF under reflux condition and then poured onto crushed ice to yield the desired products which were then crystalized out using chloroform (Scheme 1).
4-((4,6-dichloro-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one was synthesized by reported process31 having melting point 208-210°C. 1H-NMR of 4-((4-chloro-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one showed CH proton at 5.65 δ ppm and NH at 7.8 δ ppm. IR signal appeared at 1742 due to presence of C=O group. These data confirmed the formation of compound 4. 1H-NMR signal of 4-((4-((4- methoxyphenyl)amino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one 6b appeared in δ ppm, -OCH3 proton showed at 3.80. Proton present at position 3 of coumarin appeared at 6.43. NH proton at 8.97 and NH of aromatic aniline was appeared at 9.95 which resemble to the formation of trisubstituted 1,3,5-triazine. The IR signals of C=O and NH were observed at 1725 and 3432 cm-1, respectively. The physical properties of newly synthesized compounds are depicted in Table 1. Among the synthesized compounds, some compounds have been screened for their antimicrobial activity and data are shown in Table 2.
| Entry | R | Yield in % | Melting range |
|---|---|---|---|
| 6a | H | 82 | 248-250 |
| 6b | 4-OCH3 | 85 | 251-253 |
| 6c | 3-Cl | 78 | 170-172 |
| 6d | 4-NO2 | 80 | 220-222 |
| 6e | 4-Br | 85 | 218-220 |
| 6f | 4-F | 75 | 258-260 |
| 6g | 4-Cl | 78 | 260-262 |
| 6h | 3-NO2 | 81 | 221-223 |
| 6i | 4-CH3 | 83 | 278-280 |
| 6j | 2-OCH3 | 84 | 245-247 |
| 6k | 2-CH3 | 86 | 252-254 |
| 6l | 2-F | 74 | 251-253 |
| 6m | 2-Cl | 80 | 232-234 |
| 6n | 2-Br | 81 | 246-248 |
Table 1: Physical properties of 4-((4-(arylamino)-6-(pyrazin-2-ylamino)-1,3,5-triazin-2-yl)oxy)-2H-chromen-2-one (6a-n)
| Entry | Gram-positive | Gram-negative | Fungi | ||
|---|---|---|---|---|---|
| Bacillus subtilis | Staphylococcus aureus | Escherichia coli | Pseudomonas aeruginosa | Aspergillus niger | |
| 6a | - | - | 3.00 | 1.50 | 3.75 |
| 6b | - | - | 3.50 | 1.75 | 5.00 |
| 6e | 3.50 | - | 3.75 | 1.75 | 4.25 |
| 6f | 3.50 | - | 3.00 | 2.25 | 3.50 |
| 6g | - | - | 3.25 | 1.75 | 4.75 |
| 6h | - | - | 3.25 | 1.75 | 4.25 |
*Zone of inhibition in mm, *Concentration 1000 microgram per ml, - =Not active.
Table 2: Antimicrobial activity of selected compounds
Antimicrobial activity
Microorganisms In the experiments five microorganisms were used. This group included Two Gram-positive bacteria: Bacillus subtilis and Staphylococcus aureus, Two Gram negative bacteria: Escherichia coli, Pseudomonas aeruginosa for antibacterial activity as well as Antifungal activity Fungi Aspergillus niger was used for culture conditions Nutrient agar or broths (Himedia PVT Ltd.) were used for bacterial cultivation. Before the experiments, all bacteria were subculture on fresh media and then incubated for 24 hours in temperature 30°C (P. aeruginosa and S. aureus) and 37°C (remaining bacteria). A. niger culture was inoculated in Potatoes dextrose agar than spore suspension was made by using tween 80 surfactant. Next, suspensions of microorganisms in saline\Tween 80 water were prepared and their density was established at a level of 0.5 according to McFarland Standard.
Determination of antimicrobial activity Antimicrobial activity of aqueous solutions of substrates and products of chemical synthesis was determined by well diffusion assay. Suspensions of microorganisms were overlaid with agar media and after medium solidification; the wells (10 mm in diameter) were cut with sterile cork borer. To the wells 100 μl of substrates and surfactants solutions were introduced. The plates were incubated for 24 h at the temperature of 30°C or 37°C depending on the indicator microorganism.
After incubation the diameter of inhibition zones were measured in millimeters. Tests were performed in triplicate and the mean values are presented.
Conclusion
We have demonstrated an easy and conventional method for the synthesis of novel 4-hydroxy coumarin and 2-amino pyrazine bearing 1,3,5- triazine derivatives with good to high yields. The present process comprises easy and clean workup which gave desired product with good purity. Among all compounds, six compounds were screened against gram positive and gram negative bacteria and fungi and examined zone of inhibition. Compound 6e was found active against Gram-positive and Gram-negative bacteria. However, all compounds have moderate inhibition against fungi A. niger.
Acknowledgement
The authors are thankful to Shree M. & N. Virani Science College for providing laboratory facility and Biotechnology Dept. of Pramukh swami science & H. D. Patel arts college, Kadi for providing biological activity.
References
- M.M. Abdou, R.A. El-Saeed, S. Bondock, Arabian Journal of Chemistry., 2015.
- A.K. Arya, K. Rana, M. Kumar, Lett. Drug Des. Discov., 2014, 11(5), 594-600.
- M. Larsen, H. Kromann, A. Kharazmi, S.F. Nielsen, Bioorg. Med. Chem. Lett., 2005, 15, 4858-4861.
- Z.H. Chohan, A.U. Shaikh, A. Rauf, C.T. Supuran, J. Enzyme Inhib. Med. Chem., 2006, 21(6), 741-748.
- B.S. Kirkiacharian, E. Clercq, R. Kurkjian, C. Pannecouque, Pharm. Chem. J., 2008, 42 (5), 265-270.
- Z. Guo, T. Shi, J. Xie, H. Yu, Y. Zhong, W. Zhu, Adv. Synth. Catal., 2013, 355(13), 2538-2543.
- J.W. Hinman, W.G. Jackson, H. Hoeksema, E.C. Louis, J. Am. Chem. Soc., 1956, 78, 1072.
- L.A. Sorbera, R.M. Castaner, Drugs Future., 2001, 26, 285.
- Y.L. Chen, N.C. Chang, T.C. Wang, C.C. Tzeng, Helv. Chim. Acta., 1999, 82, 191.
- K.N. Trivedi, S.M. Desai, J. Ind. Chem. Soc., 2001, 78, 579.
- G. Bouz, M. Juhás, P. Niklová, O. Jand’ourek, P. Paterová, J. Janoušek, L. Tumová, Z. Kovalíková, P. Kastner, M. Doležal, J. Zitko, Molecules., 2017, 22, 1797.
- G. Sanjeev, K.G. Vivek, B.D. Gupta, K. Sivakumar, J. Chem. Crystallogr., 2006, 36(1), 77-82.
- B. Tyagi, M.K. Mishra, R.V. Jasra, J. Mol. Catal. A-Chem., 2008, 286, 41-46.
- A. Kultti, S. Pasonen, M. Jauhiainen, K.J. Rilla, R. Karna, E. Pyoria, R. Tammi, M. Tammi, Exp. Cell. Res., 2009, 315, 1914-1923.
- D. Murray, J. Mendez, S.A. Brown, The natural coumarins: occurrence, chemistry and biochemistry, Wiley, New York, 1983.
- S. Palaniappan, S.R. Chandra, J. Mol. Catal. A. Chem., 2004, 209, 117-124.
- H. Zhao, Y. Liu, Z. Cui, D. Beattie, Y. Gu, J. Agric. Food Chem., 2011, 59, 11711-11717.
- C. Zhou, J. Min, L. Zhigang, Y. Anne, D. Heather, G. Tian, Bioorg. Med. Chem. Lett., 2008, 18, 1308-1311.
- K. Srinivas, U. Srinivas, K. Bhanuprakash, K. Harakishore, U.S.N. Murthy, R.V. Jayathirtha, Eur. J. Med. Chem., 2006, 41, 1240-1246.
- K.N. Sarmah, N.K. Sarmah, K.B. Kurmi, T.V. Patel, Adv. Appl. Sci. Res., 2012, 3(3), 1459-1462.
- H.L. Ng, X. Ma, E.H. Chew, W.K. Chui, J. Med. Chem., 2017.
- N. Nishimura, A. Kato, M. Isamu, Carbohydr. Res., 2001, 331, 77.
- B. Klenke, M. Stewart, M.P. Barrett, R. Brun, I.H. Gilbert, J. Med. Chem., 2001, 44, 3440.
- Y. Iino, T. Karakida, N. Sugamata, T. Andoh, H. Takei, M. Takahashi, S.I. Yaguchi, T. Matsuno, M. Takehara, M. Sakato, S. Kawashima, Y. Morishita, Anticancer Res., 1998, 18, 171.
- D.C. Tahmassebi, T. Sasaki, J. Org. Chem., 1994, 59, 679-681.
- D.C. Tahmassebi, T. Sasaki, J. Org. Chem., 1998, 63, 728-731.
- N. Vukovic, S. Sukdolak, S. Solujic, N. Niciforovic, Food Chem., 2010, 120, 1011-1018.
- M. Mladenovic, N. Vukovic, N. Niciforovic, S. Sukdolak, S. Solujic, Molecules., 2009, 14, 1495-1512.
- N. Vukovic, S. Sukdolak, S. Solujic, T. Milosevic, Arch. Pharm. Chem. Life Sci., 2008, 341, 491-496.
- D. Patel, R. Patel, P. Kumari, N. Patel, Med. Chem. Res., 2012, 21, 1611-1624.
- R.B. Patel, K.H. Chikhalia, C. Pannecouquec, E. de Clercq, J. Braz. Chem. Soc., 2007, 18, 312-321.