Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 6
Energy Landscape View of the Amyloid Aggregator in Protein Folding Problem
Samson O Aisida1*, Collins U Ibeji2, Chibuike D Umeh1, Rasheed S Lawal1 and Doris O Okoroh3
1Department of Physics and Astronomy, University of Nigeria Nsukka, Nigeria
2Department of Industrial Chemistry, University of Nigeria Nsukka, Nigeria
3Department of Physics Federal College of education (Tech) Omoku, River state, Nigeria
- *Corresponding Author:
- Samson O Aisida
Department of Physics and Astronomy
University of Nigeria Nsukka, Nigeria
Abstract
Amyloid protein aggregation is the basis of many neurodegenerative disorders such as Alzheimer’s, Parkinson’s, type II diabetes, Huntington’s disease and cancer related diseases. These neurodegenerative diseases are associated with aberration of a specific protein affecting its structure-function processes. In this paper, we report a study of the amyloid aggregator using numerical simulations that employ a coarse-grained Monte Carlo method in combination with a diagonally-pull moves neighbourhood search strategy in order to build the hydrophobic-core using the Hydrophobic-Polar energy model on 2D lattice to investigate the misfolded proteins that are susceptible to amyloid aggregates and obtain the pathways to folding landscape. It is evident that multiple pathways which are intermediates prone are responsible for the amyloid related diseases. The simulation reveals the thermodynamics of structural transitions during aggregation and uncovers the intriguing interconnections between the aggregated prone protein and human neurodegenerative diseases. We determine the aggregation pathway by studying aggregation states of 65-mer and 85-mer globular protein and discuss the role of the energy landscape in the management of misfolded proteins. This method is highly effective with the coupled moves and simplifies the complexity of the existing Monte Carlo (MC) and makes it consistent for the native structure prediction (NSP) when compared to other state-of-the-arts approaches.
Keywords
Protein folding, Misfolding, Amyloid aggregator, Coarse-grained model, Neurodegenerative diseases
Introduction
Human diseases are known to be in the increasing order as a result of the consequences of protein aggregation and misfolding due to protein conformational disorders [1]. Proteins, the workhorse of living organisms are linear bio-polymers formed by connecting monomers (amino acids) joined together by peptide bonds into long chains executing the genetic code inscribed in the DNA. Proteins, the most basic biological units in a living cell contain twenty amino acids distinguish from each other by just a few atoms from each other [2,3]. All proteins are constructed in the same way, despite their sundry functions. Albeit, the chemical differences of the amino acids partly explain the functional diversity of proteins and the key to protein function is found in the three-dimensional (3D) structures attained by the amino acid chains. This suggests that the knowledge of protein folding and misfolding is very significant. However, Amyloid aggregators such as molten globule are critical species in protein misfolding processes and serve as the basis for many age related and the cause of some neurodegenerative diseases such as Alzheimer’s, Parkinson’s, type II diabetes, transmissible spongiform encephalopathies, hemolytic anaemia, Huntington’s disease and cancer related diseases [4,5]. Each of them share a common characteristic associated with the misfolding and subsequent aggregation into insoluble amyloid fibrils. The aberrant biosynthesis that cause them are basically the same ones responsible for a range of other debilitating conditions.
To understand the mechanism of protein folding/misfolding and the physical principles of folding reactions; experimentalists (via: X-ray crystallography [6] and Nuclear magnetic Resonance (NMR) spectroscopy ) and theoreticians (via: lattice model [7], Coarse-grained (CG) [8-10]) models and atomistic simulation) have focused their effort on analyzing small, single domain proteins (less than ≈ 110 amino acids) to show that many of this proteins fold with simple two-state kinetics in vitro [2,11,12].
The current studies of polymers with biomedical and industrial applications cannot be overemphasized. Recently, Jonathan et al. [13] described the elastic and flexible polymers using replica-exchange Monte Carlo simulation on coarse grained polymer model to obtain the structural phase-diagram of the polymer. Also, Kai and Michael [14] investigated the autocorrelation time properties of different energies and structural quantities as functions of temperatures for flexible and elastic polymers with 30 and 55 monomers using the Metropolis Monte Carlo algorithm for coarse grained model.
In this paper, we address the protein folding problem in vitro with the application of the move-biased Monte Carlo simulation in combination with diagonal-pull moves in the 2-D square lattice model to detect the folding landscape and identify the pathways in amyloid aggregated prone proteins. The computational study of new frameworks shows that intermediate (route to folding) acts as kinetic traps that will not allow the protein to fold optimally. The Sequel to this, the protein is prone to aggregation of misfolded protein which causes nuerodegenerative disorders. The rest of the paper is organized as follows. In section 2, we described the methodology. The results and discussions are presented in section 3 and a conclusion is given in section 4.
Material and Methods
Methodology
Protein folding problem (PFP)
Protein amino acid sequences are encoded in the genes, but protein structures are the keys to understanding the mechanisms that control their ultimate biological functionality. Protein folding is therefore the final step in the translation of the genetic information to biological functions. PFP, which consists of predicting the three-dimensional (3D) structure of a protein from its given sequence of amino acids stem from Christian Anfinsen’s discovery [15] that the sequence of amino acids of a naturally occurring protein uniquely specifies its thermodynamically stable native structure. PFP is one of the most important and challenging problems in biological Physics and molecular biology. This problem can in principle be done by experimental methods like X-ray crystallography or Nuclear magnetic resonance spectroscopy analysis, but unfortunately, these methods are very slow and expensive. Thus, the main objective of PFP is to find a computational approach for predicting the 3-D structure of a protein, given their linear sequence of the amino acid [16]. PFP is often approached by statistical methods which, however, have their limitations, but the physical principle of protein folding has been broadened by the application of coarse-grained model [17]. The problem of spontaneous folding of protein residues into compact 3-D structures continues to be a pursue in the purview of protein science world [18,19].
The protein folding mechanism
The protein folding mechanism may not seem as directly, biologically relevant as folding occurs spontaneously and the biological function is tied predominantly to the folded structure. The phenomenon of spontaneous folding of protein native structures gives the basic distinction between the study of protein folding physics and protein biosynthesis. Protein folding in-vitro is the most study case of pure self-organization by a physicist, where the application of physics laws enhanced the folding of the protein chains [20]. In this paper, we focus only on the protein folding in vitro where many protein molecules undergo the folding process independently. Thus, we are dealing with an ensemble of protein molecules, in which definite fractions exist in various stages of folding at any given time. The behaviour of individual molecules fluctuates from the average, even after the ensemble has reached equilibrium. To understand the physical basis of protein folding, the analysis of the time evolution of the ensemble from the perspective of statistical physics plays a vital role, instead of the evolution of a single pathway. In this work, we introduced the relative probability (RP) as the physical mechanism to determine natural probabilities of protein conformations from self-avoiding work (SAW) and to simulate the desired sequence length of the protein residues from the relative probability parameter (RPP) optimal combination due to the interactions of non-bonded monomers to obtain a conformation that is stable with unique ground state energy minimum in our model. The RP occurs when the protein residues spin in the four possible directions (i. e up, down, right and left) which must be guided to obtain the native structure and analyses the influence of the variation of these probabilities on the sequence length (i. e length of simulated protein). Thereafter, a graphical algorithm was developed to group the SAW steps into hydrophobic and polar residues according to the Hydrophobic-Polar (HP) model.
We let, 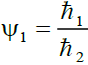 , where ℏ1 = 0.005 ... 1/2, ℏ2 = 1/4 so that 0.02 ≤ Ψ1 ≤ 2.0 (1)
, where ℏ1 = 0.005 ... 1/2, ℏ2 = 1/4 so that 0.02 ≤ Ψ1 ≤ 2.0 (1)
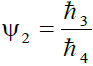 , where ℏ3 = 1/2 ... 0.005, ℏ4 = 1/4 so that 2.0 ≥ Ψ2 ≥ 0.02 (2)
, where ℏ3 = 1/2 ... 0.005, ℏ4 = 1/4 so that 2.0 ≥ Ψ2 ≥ 0.02 (2)
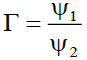 (3)
(3)
Where ℏ1, ℏ2, ℏ3 and ℏ4 are the probabilities of up, down, right and left step respectively.
Protein folding and amyloid aggregator
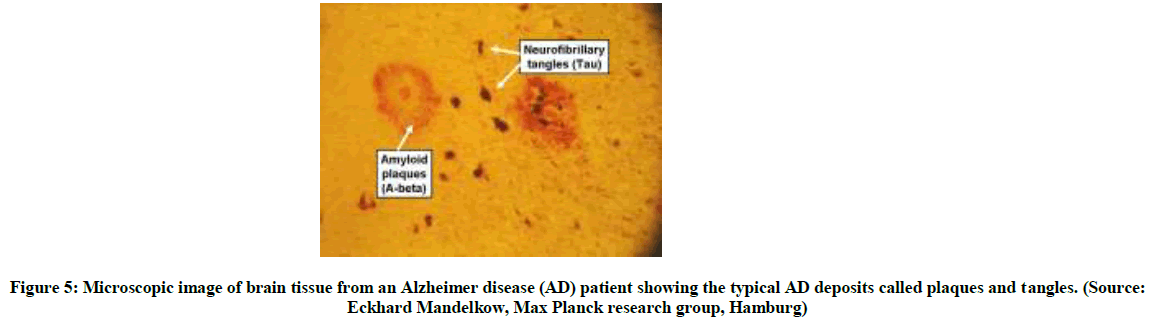
Protein misfolding gives rise to the malfunctioning of living systems. In addition to this, misfolded proteins often clump together to form a range of aggregate. These clumps (such as plaques) usually gather in the brain, and are responsible for the symptoms of the growing number of agerelated diseases such as Alzheimer’s and Parkinson’s disease as well as other neurodegenerative disorders [6]. Proteins can be involved in diseases in many different ways, despite their primary purpose of keeping the bodies functioning and healthy. The more we know about how certain proteins fold the better new proteins we can design to combat the disease-related proteins and cure the diseases. Amyloid aggregator is one of the worst ways a protein can go haywire. In this state, sticky elements within proteins emerge and seed the growth of sometimes deadly fibrils. About two decades ago, researchers had come to understand that these artificially induced fibrils had the same peculiar structure seen in disease-linked amyloid, such as the amyloid- β deposits in the brains of people with Alzheimer’s disease. Some mutations and toxins, and the cellular wear and tear associated with ageing are as a result, in misfolded proteins and those that are less protected by chaperoning and thus susceptible to amyloids. Maksym and Jim [3,21] has noted that the cooperative nature of the folding mechanisms of small, single–domain proteins protects them from misfolding and aggregation, whereas larger proteins, whose folding is less cooperative, are therefore more at risk. Greta et al., [22] demonstrated that intermediate contain low energy which can cause aggregation through exposure of hydrophobic patches in the folding process. Many diseases arise through loss of function caused by mutations that disrupt a binding site or active site of a protein or through elevated expression levels leading to increased activity of a protein. However, mutations can alternatively cause disease by destabilizing the native structure or stabilizing non-native conformations, result in the population of partly folded intermediates and leading to the side reaction of aggregation. Three notable examples, for which the relationship between the folding and the aggregation energy landscapes has been characterized in detail, are lysozyme, transthyretin and β2 – microglobuling as reviewed in ref. (186-188) of [3]. For all three proteins, partly folded intermediates have been identified that are critical for aggregation. Other illustrations of the competition between the conversion of partly folded intermediates in the native state and into aggregation include tailspike protein, luciferace, stefin, ure2, prion protein, superoxide dismutase, serpin, γ – crystalline, and SH3. Although many of these proteins forms amyloid-like aggregates that are rich in β – sheet structure, aggregate containing substantial native structure have also been observed. The amyloidogeneicity shows a significant positive correlation with hydrophobicity and sheet forming the potential and negative correlation with total charge. Hence, formation of structure and aggregates rely on very similar physico-chemical characteristics. Folding intermediates (aggregate prone) provide us with additional information of the energy landscape which is very important for understanding the fundamental steps in folding, but has limitation for small proteins [23-25].
Energy landscape theory of protein aggregator
Protein folding and unfolding can be viewed as a phase change problem from the thermodynamic point of view. Energy landscape theory (ELT) and the idea of folding funnel (FF) provide the thermodynamic framework for better understanding of the protein question [26]. In 1980s Bryngelson and Wolynes conceived the idea of ETL and FF with a conclusion that global overview of the energy landscape (EL) is indispensable for a full understanding of the folding process [27]. EL is a surface defined over a conformation space that gives the potential energy of the molecules and is the theoretical contribution to the chemical processes. This theory, which is deeply rooted in statistical mechanics of the folding process proffers a solution to Levital paradox. ELT brought about the concept of a funnel landscape to describe good folding sequences in which case there is no unique folding pathway, but a multiplicity of folding routes characterized by many local minimal and few global minima all converging towards the native structure.
Generally, according to [18,28,29], folding can be viewed as the motion of the polypeptide chain on a complex energy landscape. The energy landscape theory declares that without much loss of kinetic information protein folding can be captured by one or a small number of reaction coordinates. This reaction co-ordinate has been rarely obtained experimentally. Down-hill trajectories to the folded state are opposed primarily by chain entropy. While the landscapes for polymers with a randomly chosen order of amino acids are predicted to be rugged, the landscapes of natural proteins have been smoothed to resemble a funnel, which means that many conformations have high energy and few have low energy. This funnel topology makes predicting the mechanism of folding easy once the structure is known [30]. Monte Carlo simulation is commonly used to compute several pathways and provide a valuable tool in understanding thermodynamic mechanisms to address amyloid aggregation.
The study of protein fragments that retain the essential amyloid characteristics of the full-length sequences is attractive, because the short peptide length allows for a systematic computational investigation of aggregation kinetics and thermodynamics. Coarse-grained (CG) lattice models, on the other hand, provide the possibility of extracting general characteristics of the thermodynamics and kinetics of aggregation [9,31]. In this paper, we perform move- biased Monte Carlo (MBMC) simulation using two dimensional lattice based CG peptide model to explore the thermodynamics of structural transitions during the aggregation of 48-mer P2HP2H2P2H2-P5H10P6H2-P2H2P2-HP2H5 -and 64-mer- H12(PH)2(P2H2)2P2HP2-H2PPH2-P2HP2(H2P2)2-(HP)2H12 length sequences where ‘H’ is hydrophobic and ‘P’ polar respectively. CG is highly efficient by circumventing the atomic details to capture the important physical properties and the amino acid residues are coarse-grained by single monomer [32,33].
Move-biased Monte Carlo (MBMC)
We use local search based on self-avoiding move-biased Monte Carlo (MBMC) simulation methods by finding a sequence of 48-mer and 64-mer which satisfies the thermodynamic requirement with unique ground state energy minimal in a reasonable time through all the sets of contacts for the sequence and then calculate the energy of the conformation. In the Monte Carlo step, a move is selected at random until a move is found that conserves the unit bond lengths and does not result in more than one monomer per lattice site a process known as self-avoiding walk. Immediately the move is found, the corresponding energy change in the system ΔΨ, is evaluated using hydrophobic-polar energy model of equation (1). In lattice models, a protein of length τ and lattice L is usually considered as being defined by its sequence s=(s1,.....sτ) ∈ Lτ where the nature k(si) = -1, if subunit si is hydrophobic and 0 otherwise
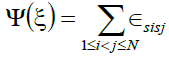 (4)
(4)
Where ∈sisj is -1 if si and sj are both hydrophobic amino acid and 0 otherwise.
This equation shows that only interactions between hydrophobic residues, (i. e given a sequence, the energy of a conformation is the number of hydrophobic-hydrophobic contacts) so called HH-contacts, are relevant for the energy calculation. All other interaction types (HP- or PPcontacts) result in no energy contribution. Therefore, if we have λ such H-H topological contacts its energy Ψ(ξ) = λ(-1), the energy evaluation focuses on hydrophobicity only.
A sequence folds in a given Monte Carlo simulation if it finds the native conformation (the compact self-avoiding chain with the lowest energy) within a reasonable small number of Monte Carlo steps. The current conformation is updated using the coupled diagonal- pull move search strategy. The MC search is based on the idea of iteratively improving a given candidate solution by exploring its local neighbourhood. In PSP the neighbourhood of a conformation can be thought to consist of slight perturbations of the respective conformation. The neighbourhood (move sets) for PSP specifies a perturbation as a feasible change from a current conformation ξ in time t to a valid conformation in time t + 1.
Hence, the neigbourhood of a conformation ξ is a set of valid conformation ξ′ that is obtained by applying a specific set of perturbations to ξ. In this paper we consider two such neighourhoods; the pull moves and the diagonal moves (corner-flip) for the 2D lattice model. The adopted method generates an initial conformation 'ξ' following a SAW on square lattice points. It places the first amino acid at (0, 0) follow by a random selection of a basis vector to place the amino acid at a neighboring free lattice point. The mapping proceeds until a SAW is found in the whole protein sequence. We compute the energy Ψ(ξ) as a SAW on square lattice point for each conformation using equation 4. We stop the process if the move is ergodic.
1. The adopted method generates an initial conformation 'ξ' following a SAW on square lattice points. It places the first amino acid at (0, 0) follow by a random selection of a basis vector to place the amino acid at a neighboring free lattice point. The mapping proceeds until a SAW is found in the whole protein sequence.
2. We compute the energy Ψ(ξ) as a SAW on square lattice point for each conformation using equation 3.3.
3. We let i = 1
4. We execute coupled (diagonal-pull) moves for all legal move positions of the ith amino acid of the current conformation ξ. If the coupled move is executed successfully, we compute the energies of the corresponding legal conformations obtained by coupled moves and pick out the conformation with the lowest energy as a newly updated conformation of, ξ expressed as ξ*
5. We compute Ψ(ξ*)
6. If the Ψ(ξ*) < Ψ(ξ), then let ξ = ξ*, Ψ(ξ) = Ψ(ξ*) and go to the last procedure; otherwise go to (7)
7. If (0 ≤ ℜ ≤ 1) < exp{[Ψ(ξ) − Ψ(ξ*)]/kBT}, where ℜ(0,1) denotes a random number between 0 and 1, then we let ξ = ξ*, Ψ(ξ) = Ψ(ξ*), and go to (9); otherwise we go to (8)
8. From the current conformation ξ, we produce the new conformation ξ* by coupled move search strategy. If ξ* is a legal conformation, then we update the current conformation ξ with ξ*, i.e we let ξ = ξ*, Ψ(ξ) = Ψ(ξ*)
9. Stop if the move is ergodic; otherwise we go to step (2)
Results
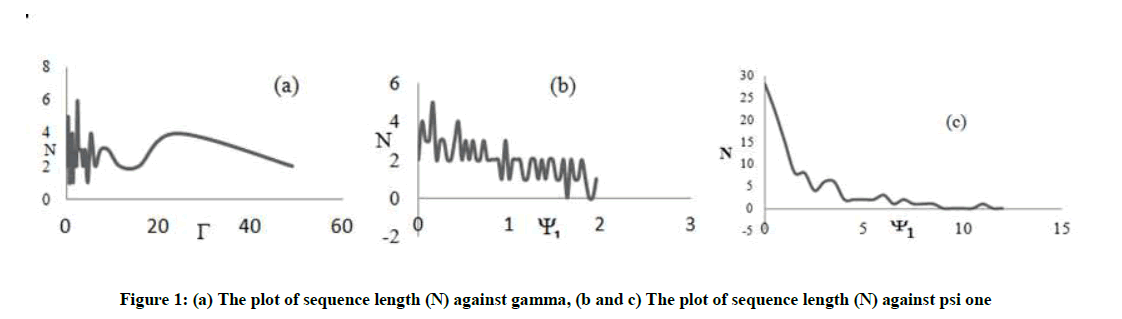
From Figure 1a, as psi two tends to zero gamma increases and eventually favour two directions the probability of up and that of down. Also the probability of a right is lower than left for low psi two; as a result of this the sequence length may be short because two directions are favoured. The fluctuation in the sequence length as a function of psi one as shown in Figure 1b is due to the other factors (directions). If all other directional probabilities are fixed; then the fluctuations will give way to a more steady variation. From Figure 1c, it is obvious that the sequence length decreases gradually as psi one increases, which confirms that the variation in the sequence length stabilizes with a reduction in the competition between the directions (for this figure we used Pd = 0.02, Pr = 0.02 and Pl = 0.25 to simulate a situation in which only the left direction is dominant).
Discussion
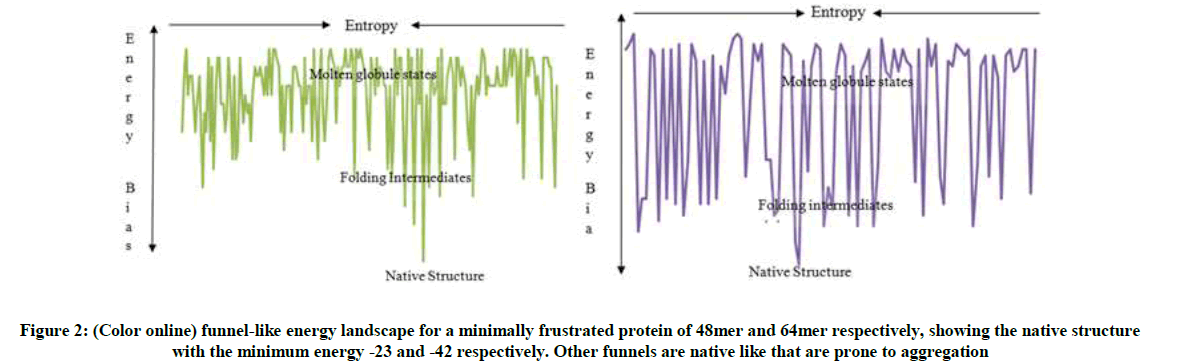
The energy landscape as shown in Figure 2 with a randomly chosen order of amino acids is very rugged and has been smoothed to resemble a funnel, with many high energy and few low energy conformations. This funnel topology makes predicting the mechanism of folding easy once the structure is known. The intermediate conformations which constitute the high energies (non-compact structure) are essential stepping-stones that guide a protein through the folding process to the native state. These intermediates are the critical species in misfolding processes (i.e an aberration from the native state) that lead to aggregation and diseases; because they expose sticky interfaces that are normally buried in the native states. The common one is the ‘molten globule’, i.e. a state possessing native-like secondary structure elements, but lacking the tight packed tertiary structure of the native state.
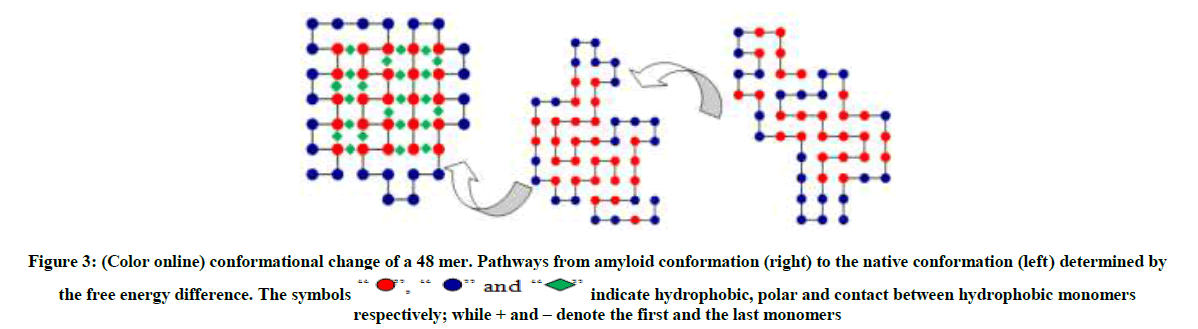
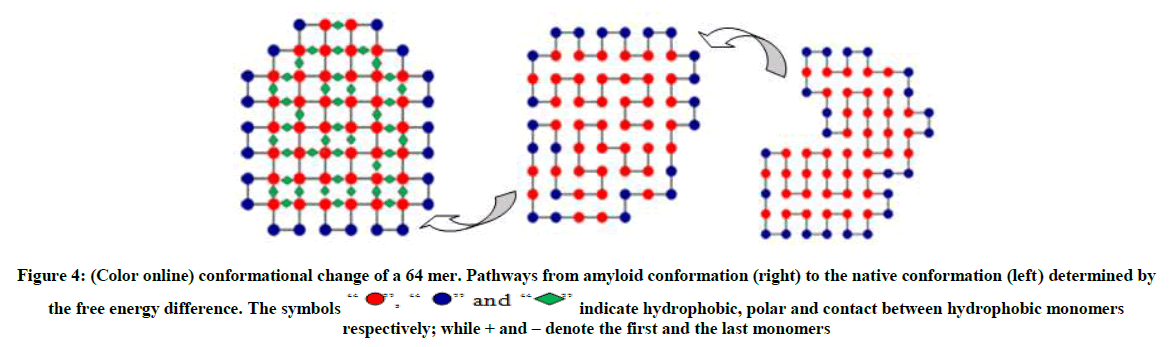
The conformation on the right as shown in Figure 3 and 4 are typical random structured coils that are amyloid prone, the structures in the middle (an intermediate) are quasi-native having the form of tertiary structure but lacking the tightly packed native structure. The polymer now has a native structure form which can function optimally as shown on the left with the ground state energy of -23 and -42 respectively obtained by MBMC. From Figures 3-5 the polymer collapses from the coil (right) to the native structure (left).
The symbols “ ”, “
”, “ ” and “
” and “ ” indicate hydrophobic, polar and contact between hydrophobic monomers respectively; while + and – denote the first and the last monomers
” indicate hydrophobic, polar and contact between hydrophobic monomers respectively; while + and – denote the first and the last monomers
Figure 3: (Color online) conformational change of a 48 mer. Pathways from amyloid conformation (right) to the native conformation (left) determined by the free energy difference.
The symbols “ ”, “
”, “ ” and “
” and “ ” indicate hydrophobic, polar and contact between hydrophobic monomers respectively; while + and – denote the first and the last monomers
” indicate hydrophobic, polar and contact between hydrophobic monomers respectively; while + and – denote the first and the last monomers
Figure 4: (Color online) conformational change of a 64 mer. Pathways from amyloid conformation (right) to the native conformation (left) determined by the free energy difference.
Because of the importance of proteins in all biological processes such as keeping our bodies functioning and healthy, it is not surprising that failure to remain correctly folded will lead to the malfunctioning of living systems and therefore involved in disease in many different ways. From Figure 2, one of the characteristic features of the misfolded protein is that they are often given rise to the deposition of proteins in the form of amyloid fibrils (one of the types of aggregates that can be formed by a protein) and plaques. The aggregate prone native like structures are structurally unstable and contain amyloid aggregate which responsible for neurodegenerative diseases. Misfolded and aggregated proteins are toxic to cells because their accumulation interferes with a variety of cell functions, hence it give rise to many diseases through loss of function caused by mutations by destabilizing the native structure leading to malfunctioning of living systems.
Disordered proteins often show significant association with aggregation (a family of amyloidoses) involved in neurodegenerative diseases. These amyloid diseases as shown in Table 1 are classified by the causative protein and disordered prediction percentage that forms the amyloid and are usually intractable. They are highly ordered deposits of misfolded protein, which often originate from full-length proteins. Diseases associated with protein misfolding and aggregation are among the most debilitating, socially disruptive, and costly in the modern world, and they are becoming increasingly prevalent as our lifestyles change and our populations age. Understanding the cause of the transition and the structural details of aggregated states will provide the insight required for designing successful intervention strategies against the diseases [31,34].
| Disease | protein | region | Disorder by Prediction % | characteristic Pathology | |
|---|---|---|---|---|---|
| Alzheimer’s | Amyloid protein | A β peptide | 28.6 | Disordereed | Extracellular plaques; tangles in neuronal cytoplasm |
| Huntington’s | Huntingtin | poly Q region | 30.4 | Disordereed | Intranuclear Inclusions and cytoplasmic aggregates |
| Parkinson’s | α-Synuclein | Whole protein | 52.2 | Disordered | Lowy body formation |
| Prion disease | prion | Whole protein | 61.0 | Half disordered | Spongiform degeneration; extracellular plaques; amyloid inside and outside neurons |
Table 1: Best known Amyloid diseases caused by aberration in the folding process adapted and modified from [34]
Conclusion
In this paper, looking at the general mechanism of protein folding in vitro and the impact of protein aggregation that leads to neurodegenerative disorder. Employing the move-biased Monte Carlo algorithm coupled with diagonal-pull move, we have performed computer simulations using two dimensional lattice based Coarse-Grained peptide model to explore the thermodynamics of structural transitions. We used the energy landscape concept to describe good folding sequences in which case there is no unique folding pathway, but a multiplicity of folding routes characterized by many local minimal and few global minima all converging towards the native structure. Over the years, many researchers are interested in the final structure of the folding and not how it got there. From Figures 3 and 4, it is believed that the final structure does not cause diseases, but rather the intermediate steps along the way are prone to amyloid aggregates which are responsible for the toxicity found in the disease, hence the path along the folding play a much more role than the final structure.
References
- P.J. Tuomas, V. Michele, M.D, Christopher. Phys. Today., 2015.
- T.S. Daniel, S. Stefan, B. Michael, Int. J. of Modern Phys. C, 2012 8(23), 1240004.
- T. Maksym, I.S. Laura, Arch. Biochem. and Biophys., 2013, 531, 14.
- L.O. Kenneth, B. Michael, S. Birgit, Proteins.,2013, 81, 1155.
- O.L. kenneth, B. Bogdan, B. Michael, S. Birgit, Phys. Proce., 2014, 53, 95.
- J. Kendrew, G. Bodo, H.R. Dintzis, W.H. Parrish, D. Phillips, Nature., 1953, 181, 666.
- R.A. Broglia, G. Tiana; Physical Models for Protein Folding and Drug Design, Germany, Frankfurt Institute for Advanced Studies, 2003, 23.
- N. Marian, Ph.D Thesis, Cornell University, Cornell, New York, 2006.
- V. Thomas, G. Jonathan, M. Bachmann, J. Chem. Phys., 2015, 142, 104901.
- H. M. Paulo, B. Michael, Acta Phys. Polo. B., 2015, 6(46).
- G. Nobuhiro, Progress of theoretrical Physics Supplement., 2007, 170.
- J. Guo, D. Mi, Y. Sun, Phys. A., 2010, 389, 761.
- G. Jonathan, N. Thomas, V, Thomas, M. Bachmanna, Phys. Proce., 2014, 53, 50.
- Q. Kai, B. Michael, J. Chem. Phys., 2014, 141, 074101.
- C. Anfinsen, Sci., 1973, 181, 223.
- Y. Zhang, J. Skolnick, Proc. natl. acad. Sci., 2005, 102, 1029.
- S. Erik, Ph. D. Thesis, Lund University, Lund, Sweden, 2000.
- B.S. Ginka, M.D. Ronan, N.V. Buchete, J. Kubelka, Bioch. et Biophy. Acta., 2011, 1814.
- Y. Zhang, Curr. Opin. Struct., 2008, 18, 342.
- A.G. Finkelstein, Phys. of life rev., 2004, 1, 23.
- S. Jim, Nature., 2010, 464, 828.
- H. Greta, P.W. Soren, C.N. Celestine, S. Kristian, G. Stefano, Biochem. and Biophy. Res. Comm., 2012, 42, 550.
- A. Fernandez, J. Kados, L. Scott, Y. Goto, R. Berry, Proc. Natl. Acad. Sci., 2003 100, 6446.
- F. Chiti, M. Stefani, N. Taddei, G. Ramponi, C. Dobson, Nature., 2003, 424, 805.
- R. Linding, J.R. Schymkowitz, F. Diella, L. Serrano, J. Mol. Biol.,2004, 342, 345.
- H. Scheraga, In: R. Broglia, L. Serrano, G. Tiana (Edi.), Proceeding of the international School of Physics Enrico Fermi, Amsterdam (IOS Press, Amsterdam 2003), 2007.
- N. Hugh, G. E. Angel, N.O. Jose, Proc. Natl. Acad. Sci.,1998, 95, 5921.
- T. Wust, D. Landau, C. Gervais, Y. Xu, Comp. Phys. Comm.,2009, 180, 475.
- W.L. Ying, W. Thomas, L.P. David, Comp. Phys. Comm.,2011, 182, 1896.
- R.A. Broglia, L. Serrano, G. Tiana, Proceedings of the international school of Physics Enrico Fermi, IOS Press, Societa Italiana Di Fisica, 2007.
- O. Judith, O. Ferenc; Protein Folding and Misfolding: Neurodegenerative diseases, Netherland, Springer, 2009.
- B. Tristan, D. Markus, J. chem. Phys.,2009, 130, 235106.
- C. Yantao, Z. Qi, D. Jiandong, J. Chem. Phys.,2004, 120, 7.
- C.M. Dobson, Nature.,2002, 418, 729.