High pressure Isothermal Equation of state for Chalcogenides

Abstract

Theoretical calculations have been done to study the high pressure behaviour of chalcogenides CeS, CeSe, CeTe by using Shanker EOS, Tait EOS, Vinet EOS and Birch-Murnaghan EOS. These EOSs are also tested for the basic requirements revealed from the fundamental thermodynamics for chalcogenides in the limit of extreme compressions, as given by Stacey. It is found that at low compressions, the three EOSs viz Tait EOS, Vinet EOS and Birch-Murnaghan EOS gives exactly the similar results but Shanker EOS deviate from other three. Further we notice that Shanker EOS is less useful to calculate elastic properties of Chalcogenides in comparison to Tait EOS, Vinet EOS and Birch-Murnaghan EOS.

Keywords

Chalcogenides; EOS; Bulk modulus; High pressure

INTRODUCTION

The equation of state (EOS) of a system basically describes the relationships among thermodynamic variables such as pressure, temperature and volume. The study of equation of state for solids has been extremely useful in the field of geophysics and condensed matter physics. The isothermal EOS expresses the relation between pressure and volume at constant temperature while the relation between the volume and temperature at constant pressure is known as the isobaric EOS. However, the isochoric EOS relates temperature and pressure at constant volume.

It should be mentioned that the EOS expression for pressure (P), bulk modulus (B0) and its derivatives (B0’) are not easy to obtain.

Strength and elastic properties of a solid depend on the strength of its interatomic forces. Therefore, the application of pressure which changes interatomic distance of the substances changes its physical properties. This pressure versus volume relation is known as equation of state and may be quite useful to understand the physical properties of the material. In the literature, there are a number of equations of state, and these arise from an unchecked and unverifiable assumption concerning an assumed interatomic potential, an assumed strain function, or an assumed boundary condition that cannot be tested [1]. Therefore, the fitting of the experimental pressure-volume data has been the usual practice to prove the suitability of an EOS in different class of solids. However, the fitting of data up to the small pressure range does not provide any support for the validity of the EOS beyond the fitting range due to two reasons.

(i)For small compression almost every EOS gives the results within the experimental uncertainty, as laboratory measured data are often subjected to pressure calibration errors [2].

(ii)Almost every EOS, new or old, can be fitted to a given range of data by adjusting the values of the zero pressure, isothermal bulk modulus, and its pressure derivatives [2]. the experimental values of pressure at different compresions are in current cenario having great concern as at low compression ranges the experimental value of pressure at different low compression are available but at high compression the experimental value of pressure are still lacking the equation of states provides and useful tact for obtaining pressures at different high compressions but as compressions increasing all the available equation of state does not provides the exact value of pressures at different compresions. Our perposed work will give significant path for calculating the value of pressure at different compresions for chalcoginides.

Thus, the aim of the present work is to discuss the applicability of Shanker [3], Tait [4, 5], Vinet [6], and Birch-Murnaghan EOSs [7] along with an equation of state recently formulated by Kholiya [8] as well as to check the validity of these EOSs for Stacey criterion under infinite pressure. For this purpose CeS, CeSe, CeTe is taken as an example due to the reasons that the phase transition pressure for it is greater than 300 GPa [9, 10] and a large number of experimental and theoretical studies [9-22] have done for it so a large number of data is available up to the very large pressure for the sake of comparison.

Cerium, uranium, neptunium and plutonium are on the border between the elements which have a localized magnetic moment and the elements which are non-magnetic and may even are superconductors. These elements and their compounds display numerous allotropic structures and properties which can be interpreted in terms of mixed valences or valence fluctuations which come from the unstable f orbitals.

CeO was obtained from high pressure synthesis as it cannot be obtained at normal pressure [lo]; it is metallic with a yellow luster asthe other cerium monochalcogenides. Its volume decreases very rapidly to 3 GPa above which the rate of change becomes more gradual.

To date, fossil fuels have helped in the development of human civilisation and has proved to be an invaluable economic resource. With the advancement of modern lifestyle, it is predicted that we will consume about 25 – 27 TW of energy, which is more than 80% of the energy which can be obtained from the remaining reserve of fossil fuels. Among all these different classes of materials, metal chalcogenides (compounds of sulphur, selenium, tellurium) like MoS2, MoSe2 etc., initially found their applications in CO2 reduction through electrocatalytic and thermochemical photoreduction [14]. Metal chalcogenides are well known for their good mechanical, thermal, electrical, and optical properties [15]. In chalcogens, the valence shell electronic configuration is ns2np4, which on bonding have lone pair of electrons that does not participate in covalent bonding.

Amorphous materials particularly chalcogenide glasses (Se, Te and S alloys) are promising materials for the fabrication of various solid state devices. The distinctive properties and functionalities of chalcogenide glasses make them promising materials for photonic applications. Chalcogenide glasses are transparent from the visible to the near infrared region and can be moulded into lenses or drawn into fibers. They have useful commercial applications as lenses for infrared cameras, chalcogenide glass fibers, waveguides, optical switch, as chemical and temperature sensors and phase change memories.

Method of analysis: In the current study we have used four different EOSs to study the thermo elastic properties of chalcogenides.

Shanker EOS: Shanker and Kushwah [1] haveexpanded pv² in powers of [1 − (V/V₀)] up to the quadraticterm and found that the equation works well for materialshaving pressure derivative of the isothermal bulk modulusless than four.Newly, Kholiya [8] has expanded pressure inpowers of density up to the quadratic term and achieved the EOS as

In the present study, we have also used the equation of state of Shanker, Tait, Vinet, and Birch-Murnaghan for comparison. EOS can be stated as follows (1–4):

Euler's strain represents the strain in relation to the stressed state that widely utilize in analyzing the high-pressure behavior of solids. The Eulerian strain (fe) is given by [9]:

Where V0 is the volume at atmosphere pressure and V is the volume at pressure.

 

Equations (1), (2), (3), and (4) are Shanker, Tait, Vinet andBirch-Murnaghan equation of states, respectively, and here B₀and B₀ are the bulk modulus and its first order pressure derivative at P = 0 and T = T₀, respectively, and

 

The bulk modulus can be found by

 

The first order pressure derivative of isothermal bulk modulus B’ can be find by

All these EOSs are also tested for the basic criteria which must be satisfied by an EOS for its validity and applicability as suggested by Stacey [1, 20, 21]. These criteria are as follows.

(i) In the limit → ∞, V/V0→ 0.

(ii) With the increase in pressure isothermal bulk modulus must increase continuously and in the limit of infinite pressure B → ∞.

GRÜNEISEN PARAMETERS

The microscopic definition of the Grüneisen parameter (Grüneisen 1912) is written in terms of the volume dependence of the ith mode of vibration of the lattice (ωi) and is given by [40]:

However, evaluation of all gi throughout the Brillouin zone is impossible without some lattice dynamical model or high pressureinelastic neutron scattering data.

In the past, however, when ab initio approaches were less routinely available, more approximate forms of γ were developed, all of which are based upon a number of assumptions(see e.g., Poirier 1991). Traditionally, among the various gammas, three have often been used: the Slater gamma, γS (Slater1939), the Dugdale-MacDonald gamma, γDM (Dugdale and MacDonald 1953), and the Vaschenko-Zubarev or free-volume gamma, γVZ (Vaschenko-Zubarev 1963). More recently, a correctionhas been applied to the latter, resulting in a modified free-volume gamma, γmfv, (Barton and Stacey 1985; Stacey1995) [4] (Table 1). At atmospheric pressure (taken as P = 0) they all depend solely on B0' (dB/dP at P = 0) and are given by:

The Gr��Ì?neisen parameter can be find by

 

RESULT AND DISCUSSION

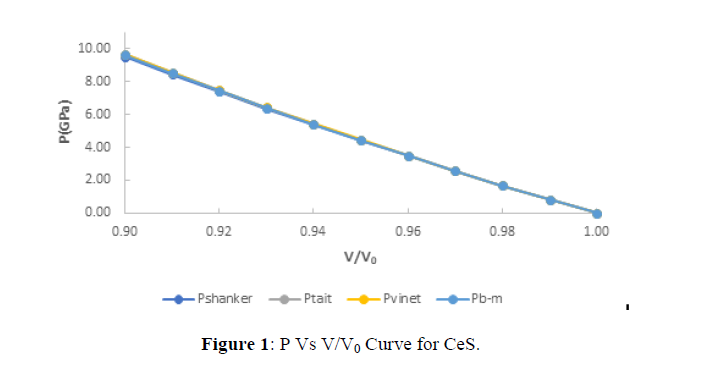
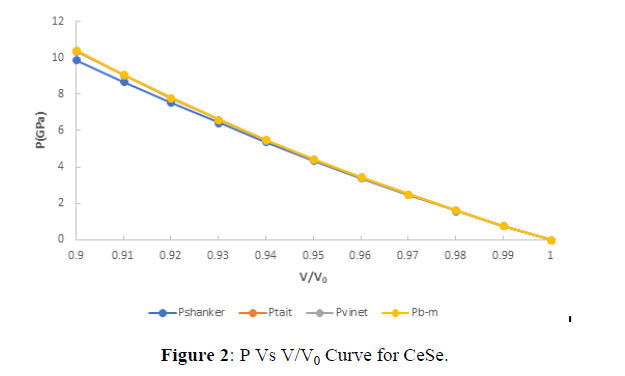
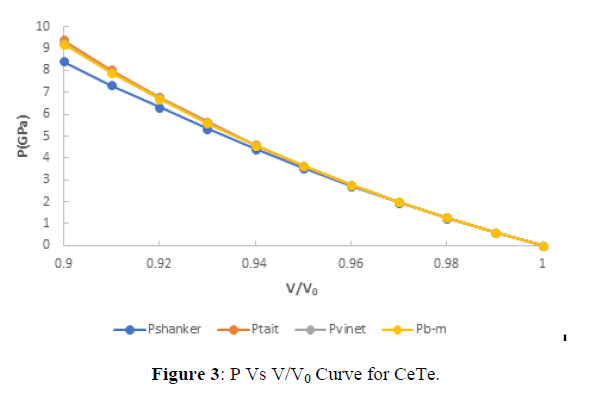
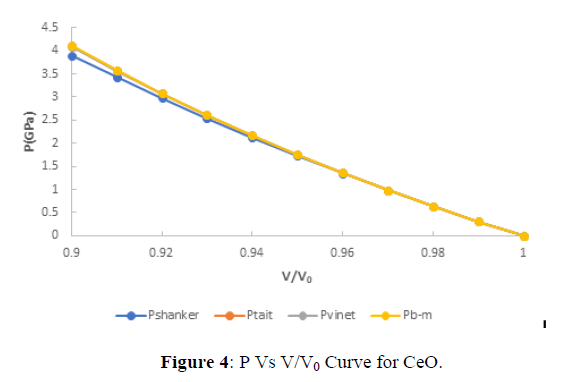
The value of pressure at different compression is shown in figures 1-4. From figures (1), (2), (3), (4), it is clear that with increasing the compression the value of pressure increases linearly which verifies the observe fact that with increasing pressures the solids gets contracted or compression ratio increases. Further from critical study of the graph it is observe that for CeS, CeSe all the four EOS corresponds well both at high as well as low compression range but in case of CeTe the two EOS viz the three EOS viz Birch-Murnaghan EOS, Vinet EOS and Tait EOS corresponds well with shanker EOS but after it the Shanker EOS starts deviating and gives this similar result in comparison to Birch-Murnaghan EOS, Vinet EOS and Tait EOS. Further in case of CeO the Birch-Murnaghan EOS, Vinet EOS and Tait EOS corresponds well at V/V0=0.94 but after it the Shanker EOS starts deviating. Hence on the basis of above discussion we can conclude that all the four EOS viz Birch-Murnaghan EOS, VinetEOS ,Tait EOS and Shanker EOS corresponds well at low compression range whereas the Shanker EOS its starts deviating with other three EOS at high compression or in other words we can say Shanker EOS is not useful for calculating pressure at different compression for chalcogenides at high compression.

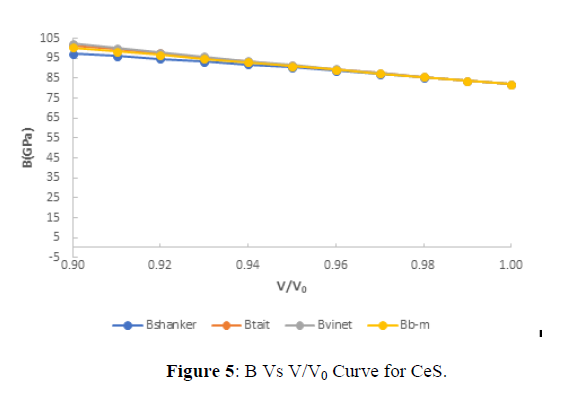
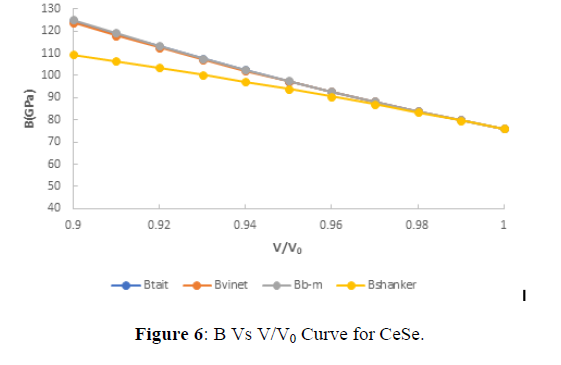
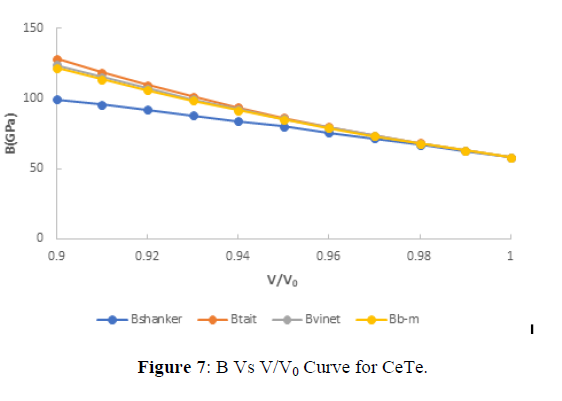
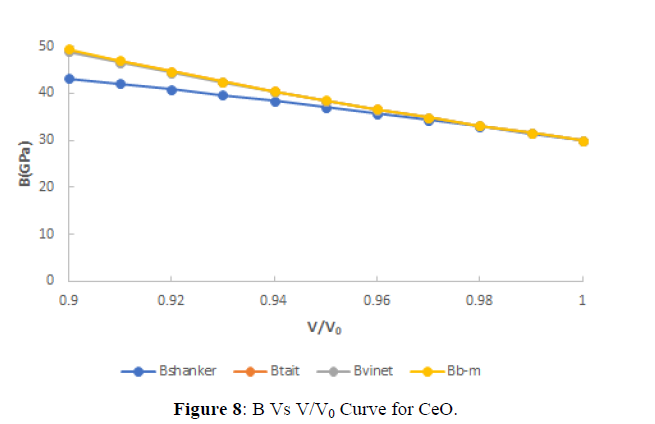
The value of Bulk modulus at different compression are shown in figures (5-8). From figures (5-8), it is clear that with increasing the compression the value of bulk modulus increases linearly which verifies the observe fact that with increasing bulk modulus the solids gets contracted or compression ratio increases. Further from critical study of the graph it is observe that for CeS, CeSe all the four EOS corresponds well both at high as well as low compression range but in case of CeTe the three EOS viz the three EOS viz Birch-Murnaghan EOS, Vinet EOS and Tait EOS corresponds well with shanker EOS but after it the Shanker EOS starts deviating and gives this similar result in comparison to Birch-Murnaghan EOS, Vinet EOS and Tait EOS. Further in case of CeO the Birch-Murnaghan EOS, Vinet EOS and Tait EOS corresponds well at V/V0=0.98 but after it the Shanker EOS starts deviating. Hence on the basis of above discussion we can conclude that all the four EOS viz Birch-Murnaghan EOS, Vinet EOS,Tait EOS and Shanker EOS corresponds well at low compression range whereas the Shanker EOS its starts deviating with other three EOS at high compression or in other words we can say Shanker EOS is not useful for calculating bulk modulus at different compression for chalcogenides at high compression.

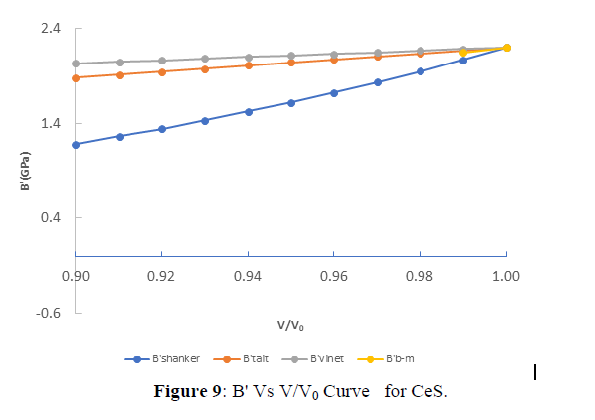
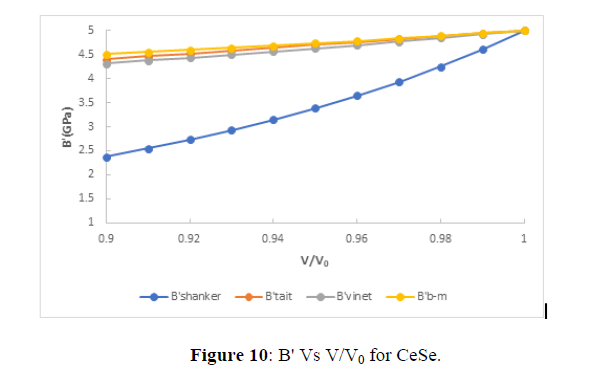
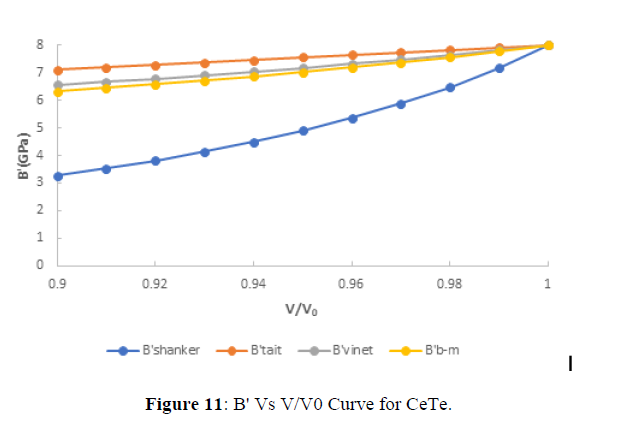
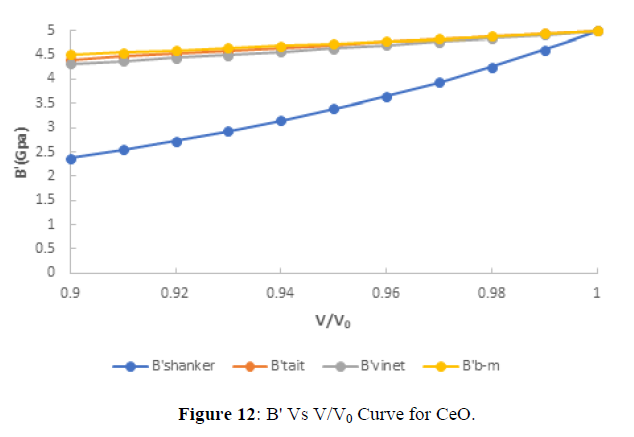
The value of first pressure derivative of bulk modulus at different compression are shown in figures (9-12). From fig.(9), (10), (11), (12), it is clear that with increasing the compression the value first pressure derivative of bulk modulus increases linearly which verifies the observe fact that with increasing bulk modulus the solids gets contracted or compression ratio increases. Further from critical study of the graph it is observe that for CeS, CeSe all the three EOS corresponds well both at high as well as low compression range but in case of CeTe the three EOS viz the three EOS viz Birch-Murnaghan EOS, Vinet EOS and Tait EOS corresponds well with shanker EOS but after Tait EOS starts deviating at point (0.98) and Shanker EOS all points are deviating. Further in case of CeO the Birch-Murnaghan EOS, Vinet EOS and Tait EOS corresponds well at V/V0=0.99 but after it the Tait EOS starts deviating at point(0.98) and Shanker EOS all points are deviating. Hence on the basis of above discussion we can conclude that all the four EOS viz Birch-Murnaghan EOS, Vinet EOS,Tait EOS and Shanker EOS corresponds well at low compression range whereas the Tait EOS and Shanker EOS its starts deviating with other two EOS at high compression or in other words we can say Shanker EOS is not useful for calculating first pressure derivative bulk modulus at different compression for chalcogenides at high compression.

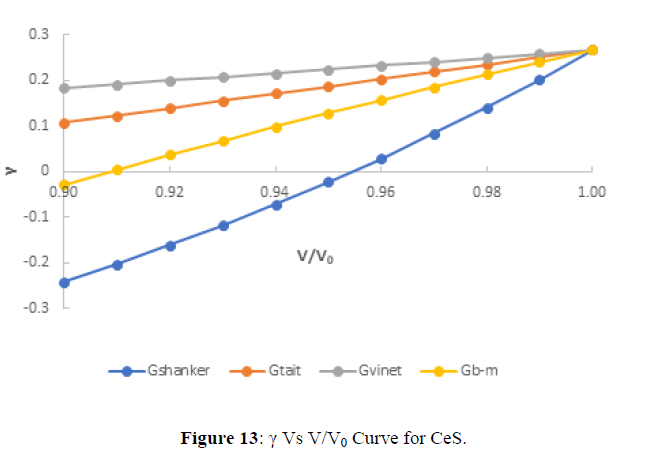
The variation of Gruneisen parameter (γ) Vs V/V0 curve for CeS is shown in figures 13. It shows that the three equations of states’s viz Vinet EOS, Birch-Murnaghan EOS and Tait EOS crorresponds well at low compression range 0.99, further with increasing compression from 0.98, The Tait EOS and Venit EOS corresponds well to each other but the Birch-Murnaghan EOS starts to deviate with them. Further, on critical analysis of figure 14 its shows that for calculating Gruneisen parameter (γ) with V/V0 the calculated value Gruneisen parameter (γ) at different compression is almost constant when it is calculated by using Tait EOS and Vinet EOS whereas Shanker EOS gives bad agreement. The above discussion shows that Birch-Murnaghan EOS is best for calculating Gruneisen parameter (γ) at different compression as compare to Tait EOS, Vinet EOS whereas the Shanker EOS gives bad agreement for calculating Gruneisen Parameter both at high as well as low compression range.

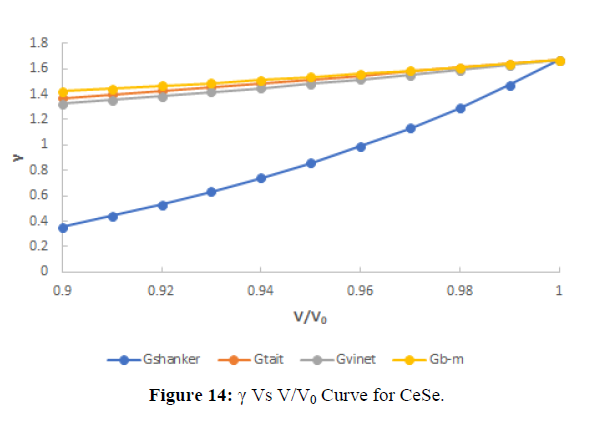
The variation of Gruneisen parameter(γ) Vs V/V0 curve (14) shows that the three equation of states’s viz Vinet EOS, Birch-Murnaghan EOS and Tait EOS crorresponds well at compression range 0.99 i.e at low compressions further with increasing compression range 0.98 the one EOS Vinet EOS are deviated. Corresponds well in comparison to Vinet EOS and Shanker EOS. Beyond V/V0=.92 Tait EOS deviates with Birch-Murnaghan EOS further on critical analysis curve its shows that for calculating Gruneisen parameter(γ) with V/V0 the calculated value Gruneisen parameter(γ) at different compression is almost constant when it is calculated by using Birch-Murnaghan EOS, the above fact also verifies the work done by Pandey etal. Hence the above discussion shows that Birch-Murnaghan EOS is best for calculating Gruneisen parameter(γ) at different compression as compare to Tait, Vinet, Shanker equation of state correspond least both at high as well as low compression region.

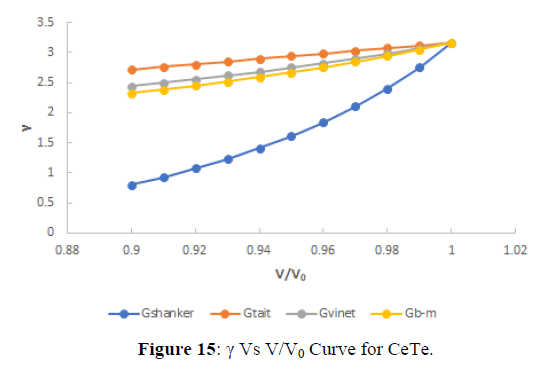
From figure 15, it is clear that the values of Gruneisen parameter obtained for CeTe by using said isothermal equation of state corresponds well at low compressions but with increasing compressions their deviation increases. The GrneisenParameter obtained by using Shanker EOS are shows maximum deviation in comparison to other EOSs. Further on critical analysis of calculated values it shows that Gruneisen parameter(γ), from Shanker EOS are not in agreement with fact that the ratio(γ/Ω) where, Ω=V/V0 is constant for solid [2]. So we can conclude that Shanker EOS is less sensitive to calculate Gruneisen parameter (γ) for chalcogenides(CeTe). The values obtained from Birch-Murnaghan EOS and Vinet EOS is very similar at low compression range (0.99). The values obtained from Tait EOS, Birch-Murnaghan EOS and Vinet EOS is in agreement with fact that the ratio (γ/Ω) is constant for solids.

The variation of Gruneisen parameter (γ) Vs V/V0 curve (16) (Figure 16) shows that the three equation of states’s viz Vinet EOS, Birch-Murnaghan EOS and Tait EOS crorresponds well at compression range 0.99 i.e at low compressions further with increasing compression from 0.99 to 0.96 the two EOS vizBirch-Murnaghan EOS and Tait EOS corresponds well in comparison to Vinet EOS and Shanker EOS. Beyond V/V0=9.6 Tait EOS deviates with Birch-Murnaghan EOS further on critical analysis curve its shows that for calculating Gruneisen parameter(γ) with V/V0 the calculated value Gruneisen parameter(γ) at different compression is almost constant when it is calculated by using Birch-Murnaghan EOS, the above fact also verifies the work done by Pandey etal. Hence the above discussion shows that Birch-Murnaghan EOS is best for calculating Gruneisen parameter(γ) at different compression as compare to Tait, Vinet, Shanker equation of state correspond least both at high as well as low compression region.

CONCLUSION

The overall discussion leads to result that all values obtained from all the four EOSs Shanker EOS, Tait EOS, Vinet EOS and Brich-Murnaghan EOS. Similar so we can conclude that all these EOS are useful to calculate pressure for chalcogenides. Further for bulk modulus Shanker EOS deviated at high pressure, so Shanker EOS is less useful to calculate bulk modulus at high pressure for chalcogenides.

Brich-Murnaghan and Tait EOS are overlap with each other even at high pressure but the two EOS highly deviate from each other. So Brich-Murnaghan and Taitare best EOS to explain first pressure derivative of Bulk modulus for CeS.

Brich-Murnaghan, Vinet and Tait EOS are overlap with each other at point 0.97, even at high pressure but the Vinet EOS slightly deviate from other, and Shanker EOS highly deviated from other three EOSs. SoBrich-Murnaghan and Tait are best EOSs to explain. First pressure derivative of Bulk modulus for CeSe.

Brich-Murnaghan, Vinet and Tait EOS are overlap with each other at point 0.99, even at high pressure but the twoEOSsVinet, Brich-Murnaghan slightly deviate from Tait EOS, and Shanker EOS highly deviated from other three EOSs. SoTait is best EOS to explain. First pressure derivative of Bulk modulus for CeTe.

Brich-Murnaghan, Vinet and Tait EOS are overlap with each other at point 0.95, even at high pressure but the two equation of statesVinet and Tait EOSs slightly deviate from each other, and Shanker EOS highly deviated from another three EOS. SoBrich-Murnaghan is best EOS to explain. First pressure derivative of Bulk modulus for CeO.

From Gruneisen parameter (γ), Vinet EOS gives best result among all four because the graph of Gruneisen parameter is straight line and slope is minimum for CeS.

Brich-Murnaghan EOS gives best result among all four because the graph of Gruneisen parameter is straight line and slope is minimum for CeSe. Tait EOS gives best result among all four because the graph of Gruneisen parameter is straight line and slope is minimumfor CeTe.

Brich-Murnaghan EOS gives best result among all four because the graph of Gruneisen parameter is straight line and slope is minimum for CeO.