Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 6
Molecular Structure, Nbo Charges, Vibrational Assignments, Homo-Lumo and Fukui Functions of Pyrazino [2, 3-D] Pyrimidine based on DFT Calculations
Ghamri M1, Harkati D1*, Saleh BA2*, Chikhaoui AR1, Belaidi S1
1Department of Chemistry, Faculty of Sciences, University of Biskra, Group of Computational and Pharmaceutical Chemistry, LMCE Laboratory, 07000 Biskra, Algeria
2Department of Chemistry, College of Science, University of Basrah, Basrah, Iraq
- *Corresponding Author:
- Harkati D
Department of Chemistry
Faculty of Sciences
University of Biskra
Group of Computational and Pharmaceutical Chemistry
LMCE Laboratory, 07000 Biskra, Algeria
Saleh BA
Department of Chemistry
College of Science
University of Basrah
Basrah, Iraq
Abstract
The optimized molecular structures, vibrational frequencies, corresponding vibrational assignments and atomic NBO charges of a biologically important molecule namely, pyrazino[2,3-d] pyrimidine have been carried out through density functional theory (B3LYP) level employing several basis sets. The results of vibrational frequencies and optimized geometric parameters were found in good agreement with the experimental data, which indicate that is planar and more stable. Moreover, the possible electrophilic and nucleophilic reactive sites were predicted by local reactivity descriptors and MEP map to describe the presence of intermolecular bonding and the hydrogen bonding interaction. In addition, the design format of our molecule present an opportunity to reveal the electron density profile by using the FMOs analysis and other electronic structure parameters such as ionization energy (I), Electron affinity (A), Global hardness (η), Chemical potential (μ), Electrophilicity index(ω), Electronegativity (X), Softness (S).
Keywords
Vibrational spectroscopy, Fukui function, NBO charge, DFT, FMO.
Introduction
One of the main objectives of organic and medicinal chemistry is to design, synthesize and produce molecules possessing value as human therapeutic agents. Compounds containing heterocyclic ring systems are of great importance receiving special attention as they belong to a class of compounds with proven utility in medicinal chemistry [1]. Pteridines, structurally the term “pteridine” describes the pyrazino [2,3-d] pyrimidine nucleus, which belong to a class of nitrogen heterocyclic compound present in a wide range of living systems. In the last century, Frederick Gowland Hopkins isolated a yellow pigment from the English Brimstone butterfly and a white pigment from the cabbage white butterfly [2].
These pigments in crystalline form and named them according to their colors, xanthopterin and leucopterin respectively [3]. There after isoxanthopterin and erythropterin were isolated from tropical butterflies and the isolation of pteridin europterin (later to be recognized as xanthopterin) from human urine [4]. In insects, they occur as metabolic end products and function as cofactors in hydroxylation reactions and as pigments. They are localized in the cuticle, wing scales, hypodermis, compound eyes, nervous system, light organ (of Lampyridae) and numerous other structures. The kind and quantity of pteridines found in insect tissues vary with developmental stages [5]. Although less symmetric, pteridine is of great intrinsic interest since it is the parent compound of a very large family of biologically important compounds [6]. So some pteridine derivatives are practically used in the chemotherapy or diagnosis of various diseases. Pteridines play an essential role in growth processes and the metabolism of one carbon unit as cofactors in enzyme catalysis and in biological coloration [7]. Many synthetic pteridines proved useful in medicine as anticancer, antiviral, antibacterial and diuretic drugs [8].
Conceptual Density Functional Theory [9-12] (DFT) is a very elegant way to describe chemical processes and provides a powerful theoretical framework for the study of both reactivity and selectivity [12]. In addition, Density functional theory methods offer an alternative [13] use of inexpensive computational methods which could handle relatively large molecules [14-16] and has been favorite one due to its great accuracy in reproducing the experimental values of molecular geometry, vibrational frequencies, atomic charges, etc. [17-29]. Thus, the present study is destined to study molecular geometry, electronic properties, NBO atomic charges, reactive sites by molecular electrostatic MEP/local reactivity descriptors, frontier molecular orbitals (FMOs) and the theoretical calculation of vibrational properties which is used to understand the spectra of large number of donor-acceptor systems [30-32]. All of these calculations have been carried out by Density Functional Theory (DFT).
Materials and Methods
Computational details
For the quantum chemical calculations, the Hyper Chem program package version 8.08, [33] was used to get the initial geometry optimization of pteridine which leading to energy minima and are achieved by using Molecular Mechanics Force Field (MM+) followed by semi-empirical PM3 method with a gradient norm limit of 0.1 kcal/Å for the geometry optimization. Then, a parallel study has been performed using Gaussian 09 program package, [34] gradient-corrected DFT with Becke 3 exchange [35] and Lee-Yang-Parr correlation functions (B3LYP) [36] with three different basis sets 6-311G, 6-311G (d,p) and 6-311G++(d,p), the overall view of pteridine with atom numbering is stimulated by MarvinSketch 6.2.1 software [37].
In the next step, the vibrational frequencies are calculated and scaled by the appropriate factor, the corresponding IR intensities, Raman activity of title molecule and the vibrational wavenumber assignments have been carried out by the GaussView 05, [38] and the Avogadro 1.0.1 software [39]. The electronic properties such as HOMO and LUMO energies were determined by the DFT approach. For obtaining chemical reactivity of the molecule, the molecular electrostatic potential (MEP) surface and the frontier molecular orbitals (FMOs) were visualized by the Gauss View 05 software, Fukui functions were calculated using Natural Bond Orbital (NBO) analysis by doing the single point energy calculation of N, N − 1 and N + 1 species of the molecule with same basis set 6-311G for analysis of molecular orbitals, the Gauss-Sum 3.0 program [40] was used to simulate the density of states (DOS) spectrum.
Results and Discussion
Molecular geometry analysis
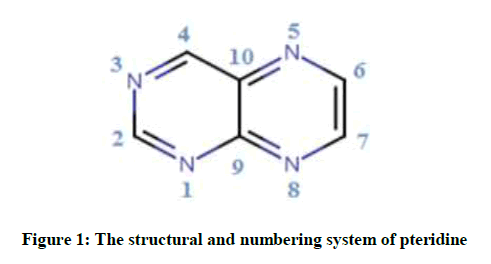
The calculations of geometrical parameters of title compound were carried out calculated by the DFT/B3LYP method, in conjugation with three different basis sets 6-311G, 6-311G (d,p) and 6-311G++ (d,p). The results are listed in Table 1. Figure 1 depicts the overall view of pteridine with atom numbering.
| Parameters | EXP | DFT/B3LYP | ||
|---|---|---|---|---|
| 6-311G | 6-311G(d,p) | 6-311G++(d,p) | ||
| Bond length (A°) | ||||
| N(1)–C(2) | 1.304 | 1.3271 | 1.3133 | 1.3133 |
| N(1)–C(9) | 1.361 | 1.3712 | 1.3559 | 1.3558 |
| C(2)–N(3) | 1.364 | 1.3793 | 1.3633 | 1.3631 |
| C(2)–H(11) | 1.01 | 1.0776 | 1.0858 | 1.0858 |
| N(3)–C(4) | 1.35 | 1.3283 | 1.3126 | 1.3127 |
| C(4)–C(10) | 1.399 | 1.4171 | 1.4172 | 1.4176 |
| C(4)–H(12) | 1.1 | 1.0812 | 1.0875 | 1.0874 |
| N(5)–C(6) | 1.308 | 1.3281 | 1.3121 | 1.3118 |
| N(5)–C(10) | 1.384 | 1.3753 | 1.3594 | 1.3589 |
| C(6)–C(7) | 1.398 | 1.4231 | 1.4241 | 1.4245 |
| C(6)–H(13) | 1.09 | 1.0806 | 1.0866 | 1.0865 |
| C(7)–N(8) | 1.286 | 1.3289 | 1.3122 | 1.3119 |
| C(7)–H(14) | 0.87 | 1.0812 | 1.0876 | 1.0874 |
| N(8)–C(9) | 1.359 | 1.3744 | 1.3614 | 1.361 |
| C(9)–C(10) | 1.392 | 1.419 | 1.4189 | 1.4195 |
| Bond angle(°) | ||||
| C(2)–N(1)–C(9) | 115.2 | 116.5942 | 116.1787 | 116.3381 |
| N(1)–C(2)–N(3) | 129 | 126.6008 | 127.9528 | 127.7701 |
| N(1)–C(2)–H(11) | 108 | 117.5376 | 116.7988 | 116.898 |
| N(3)–C(2)–H(11) | – | 115.8617 | 115.2484 | 115.3318 |
| C(2)–N(3)–C(4) | 115.7 | 117.0518 | 116.2098 | 116.3617 |
| N(3)–C(4)–C(10) | 119.8 | 121.4228 | 122.0316 | 121.9644 |
| N(3)–C(4)–H(12) | 116 | 118.7996 | 118.8683 | 118.7382 |
| C(10)–C(4)–H(12) | – | 119.7776 | 119.1002 | 119.2974 |
| C(6)–N(5)–C(10) | 114.5 | 116.1983 | 115.3681 | 115.5034 |
| N(5)–C(6)–C(7) | 123 | 121.9983 | 122.3063 | 122.2295 |
| N(5)–C(6)–H(13) | 124 | 117.2294 | 117.6232 | 117.7226 |
| C(7)–C(6)–H(13) | – | 120.7723 | 120.0705 | 120.048 |
| C(6)–C(7)–N(8) | 123.4 | 122.8506 | 123.3538 | 123.2931 |
| C(6)–C(7)–H(14) | – | 120.4038 | 119.5447 | 119.5018 |
| N(8)–C(7)–H(14) | 113 | 116.7456 | 117.1015 | 117.2051 |
| C(7)–N(8)–C(9) | 116.4 | 116.3418 | 115.6552 | 115.7876 |
| N(1)–C(9)–N(8) | – | 118.3447 | 118.225 | 118.3628 |
| N(1)–C(9)–C(10) | 121.2 | 120.916 | 121.0035 | 120.936 |
| N(8)–C(9)–C(10) | 120.9 | 120.7393 | 120.7715 | 120.7012 |
| C(4)–C(10)–N(5) | – | 120.7139 | 120.8313 | 120.8851 |
| C(4)–C(10)–C(9) | 119.1 | 117.4144 | 116.6236 | 116.6297 |
| N(5)–C(10)–C(9) | 121.8 | 121.8716 | 122.5451 | 122.4852 |
Table 1: The experimental and theoretical bond lengths (A°), bond angles (°) and dihedral angles (°) of pteridine
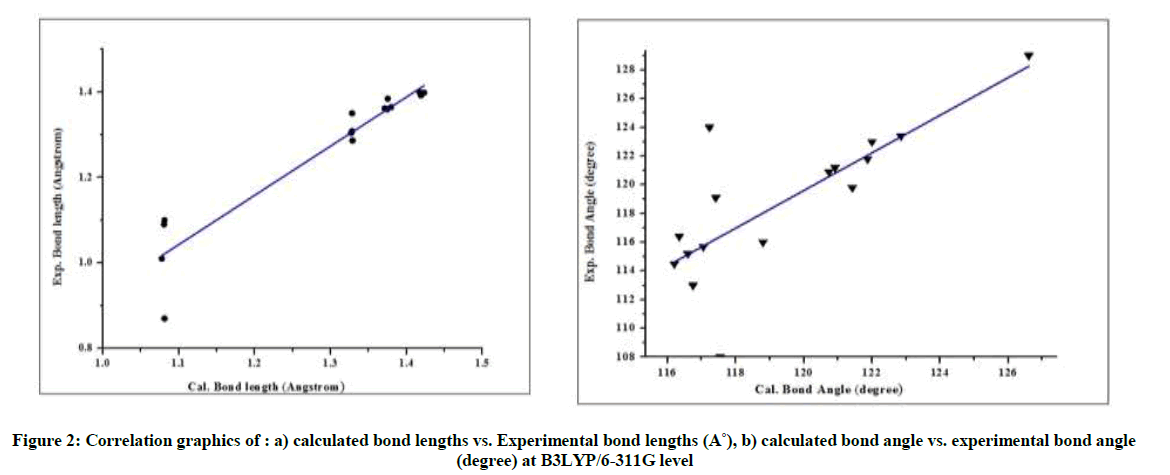
A close look at Table 1 indicates that our theoretical results are agreed with the available experimental data [41]. Plotting of the theoretical results versus the experimental ones indicates robust linear dependencies (Figure 2). The values of the correlation coefficients (r) were 0.325(6- 311G), 0.236 (6-311G (d, p)) and 0.654(6-311G++ (d, p)) for bond lengths; and the bond angles were 0.325(6-311G), 0.236 (6-311G (d, p)) and 0.654(6-311G++ (d, p)). Hence, these figures suggest that the B3LYP/6–311G bond lengths and bond angles are well fitted to X-ray experimental data, with the correlation coefficients R=0.99635 and R=0.56786 respectively. Although there are no experimental bond dihedral angles, the calculated dihedrals are present within the same table. The dihedrals angles of this molecule vary between 0° and 180° degree which explain that the geometry of pteridine is planar, which make this conformation more stable.
Atomic charges
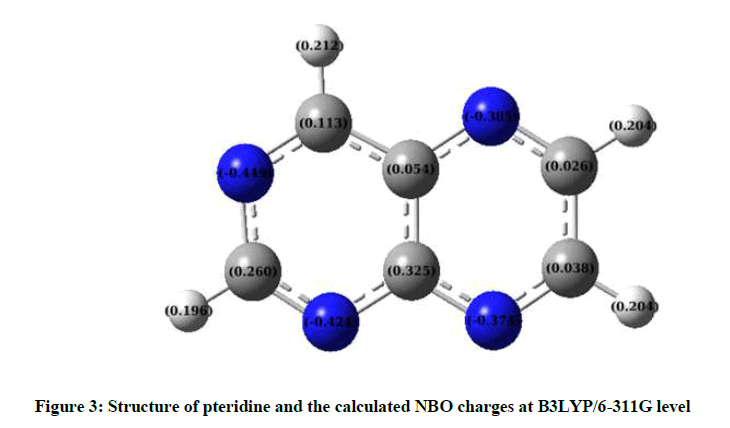
Natural Bond Orbital (NBO) analysis employs a more sophisticated scheme that uses the concept of natural orbitals and occupation-based symmetric orthogonalization that leads to more robust results. The net result of NBO analysis is that the total density is broken into localized contributions associated with individual atoms giving rise to natural charges and further into 1-center (lone pairs) and two-center (bonds) pieces. This leads to a straight toward determination of Lewis structures. NBO also allows one to determine hybridization of the AOs contributing to a particular bond [42-43]. Atomic net charges were calculated applying the natural bond orbital (NBO) analysis [44-45] at the B3LYP/6–311G level of calculation.
Figure 3 shows the atomic NBO charges. The magnitudes of the carbon atomic charges are found positive and C (9) has maximum positive atomic charge values of about 0.325 electron. Whereas the magnitudes of charges on nitrogen atoms are found negative and the maximum negative atomic charge was obtained for N (3), -0.449 electron. In addition, the magnitudes of the hydrogen atomic charges are arranged in an order from 0.196 to 0.212 electrons.
Vibration analysis
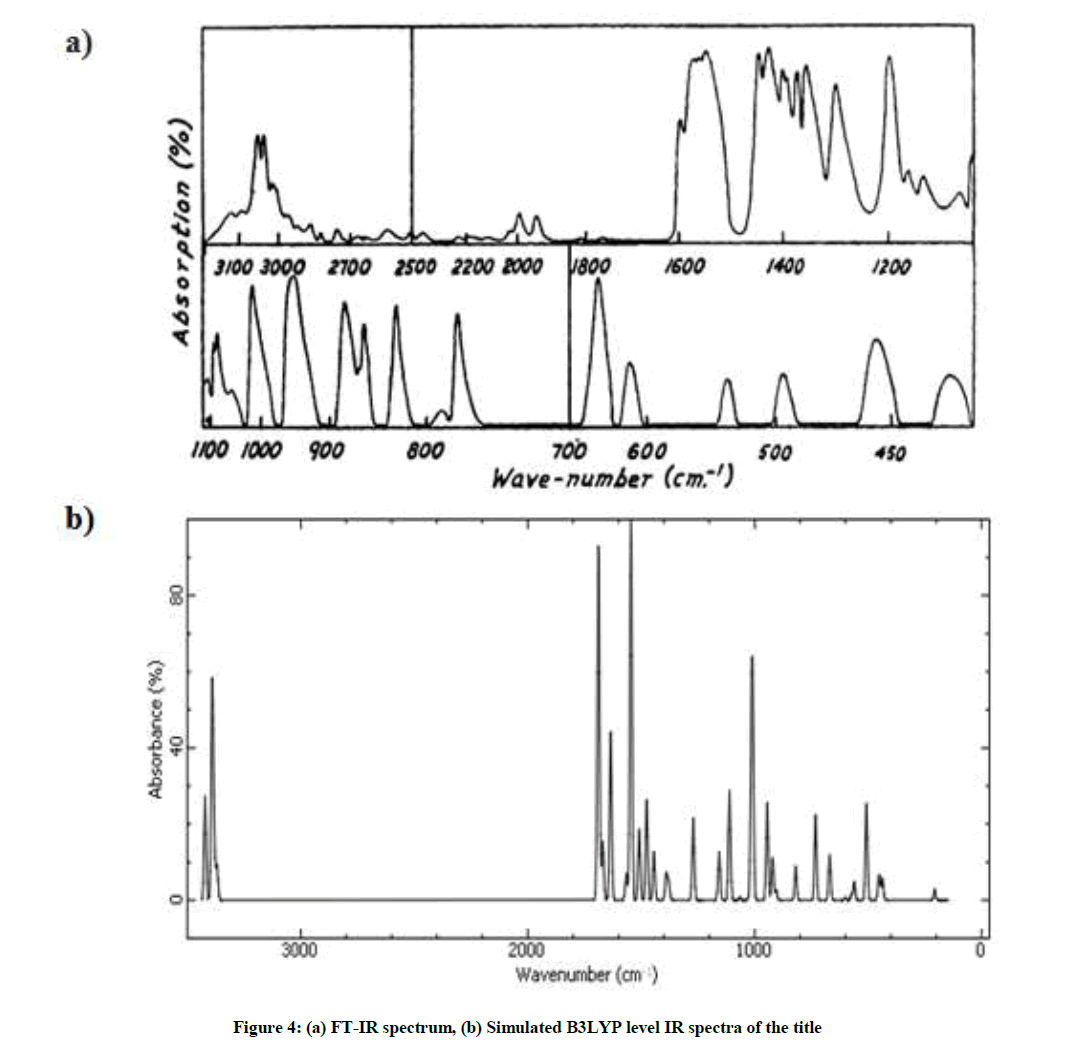
The molecule pteridine consists of 14 atoms and it possesses thirty-six possible modes of vibration, hence the molecule being of low symmetry, most of these vibrations should be active in the infrared [46]. FTIR spectrum of the investigated compound was measured in the 4000-400 cm-1 region and the vibrational frequencies of the compound were calculated in region 4000-0 cm-1 by using B3LYP/6-311Gmethod (Figure 4).
Then Table 2 presents the detailed vibrational assignment scaled by the factors 1.06 with observed wavenumbers, Infrared Radiation (IR) intensities and Raman activity of title molecule, respectively. All compared data have been shown to be in a good agreement to each other for the most stable optimized structure of the pteridine molecule.
| Assignment | Experimental frequencies [46] | Calculated frequencies (cm−1) | ||
|---|---|---|---|---|
| B3LYP 6–311G | ||||
| Theoretical frequency | IR intensity (km/mol) | R activity (Å4/amu) | ||
| γ NCH | - | 159.76 | 0.011 | 0.154 |
| γ (Pym-Pyz) | - | 195.07 | 1.803 | 0.452 |
| γ CH (Pym) | - | 412.52 | 3.462 | 4.02 |
| β CH (Pym) | 434 | 426.42 | 4.096 | 0.265 |
| γ CH (Pym-pyz) + γ CCH ( Pym) | 455 | 478.63 | 15.621 | 0.336 |
| γ NCN (Pym-Pyz) + γ CH ( pym) | 497 | 529.34 | 2.914 | 0.238 |
| β CNC (Pym) + β CCN (Pyz) | 533 | 540.7 | 0.769 | 12.18 |
| β NCC (Pyz) + β CNC (Pyz) | 616 | 567.08 | 0.324 | 9.089 |
| β CNC (Pym-Pyz) + β CCN (Pym) | 653 | 631.48 | 7.327 | 2.082 |
| γ CH (Pym-Pyz) | 777 | 690.19 | 13.785 | 0.407 |
| β CH (Pym-Pyz) + υ C=C (Pym-Pyz) | 795 | 772.9 | 5.476 | 31.956 |
| γ CH (Pym-Pyz) | 822 | 853.96 | 1.565 | 1.003 |
| β CNC (Pym) + β CCN (Pyz) | 860 | 868.95 | 6.843 | 0.282 |
| γ CH (Pyz) | 882 | 891.45 | 15.743 | 0.256 |
| β NCC (Pyz) + β NCH (pym) | 933 | 951.55 | 24.477 | 0.397 |
| γ CH (Pym) | 1015 | 956.62 | 24.095 | 0.23 |
| γ CH (Pym) | 1056 | 1003.39 | 0.377 | 0.53 |
| β CH (Pyz) | 1085 | 1008.29 | 0.003 | 2.461 |
| β (Pym-Pyz) + υ C=C (Pyz) | 1092 | 1048.04 | 17.735 | 3.926 |
| β (Pym-Pyz) + υ C-N (Pym) | 1109 | 1090.91 | 7.812 | 12.828 |
| β (Pym-Pyz) + υ C-N (Pym-Pyz) | 1158 | 1181.19 | 0.022 | 0.606 |
| β NCN (Pym-Pyz) + β NCC (Pym-Pyz) | 1197 | 1198.23 | 13.273 | 0.833 |
| υ C=C (Pym-Pyz) + β (Pym-Pyz) | 1286 | 1300.82 | 2.906 | 11.858 |
| β CH (Pym-Pyz) | 1348 | 1310.92 | 4.28 | 0.73 |
| β CH (Pym) + υ C=C (Pym-Pyz) | 1368 | 1362.42 | 7.83 | 68.004 |
| β CH (Pym-Pyz) | 1391 | 1392.24 | 16.222 | 47.435 |
| β CH (Pym-Pyz) | 1400 | 1423.32 | 11.406 | 25.691 |
| β (Pym-Pyz) + υ C=C (Pyz) | 1435 | 1457.74 | 61.776 | 0.247 |
| β CH (Pym) | 1461 | 1476.84 | 4.262 | 4.519 |
| β (Pym-Pyz) + υ C=C (Pym-Pyz) | 1558 | 1542.08 | 27.248 | 39.991 |
| υ C=N (Pyz) + β (Pyz) | 1573 | 1575.12 | 9.463 | 5.151 |
| υ C=N (Pym) + β (Pym) | 1580 | 1592.98 | 57.405 | 2.825 |
| υas CH (Pyz) | 3035 | 3178.71 | 5.539 | 96.235 |
| υas CH (Pym) | 3055 | 3190.47 | 7.84 | 113.199 |
| υs CH (Pyz) | 3090 | 3198.32 | 34.478 | 265.26 |
| υs CH (Pym) | 3117 | 3227.93 | 16.817 | 173.514 |
υ =stretching; υs=sym. stretching; υas=asym. stretching; β=in-plane-bending; γ=out-of-plane bending; Pym=pyrimidine; Pyz=pyrazine
Table 2: Comparison of the experimental and calculated vibrational frequencies (cm-1)
C–H vibrations
The C–H stretching vibrations of heteroaromatic structure are expected in the region 31000-3000 cm-1 [47-48]. In this study, the C–H stretching vibrations were observed at 3178.71, 3190.47, 3198.32, 3227.93 cm−1 theoretically, the corresponding modes were showed at 3035, 3055, 3090, 3117 cm−1 and 96.235, 113.1994, 265.2597, 173.514 cm−1 in FTIR and Raman, respectively.
The CH in-plane bending vibrations interact somewhat with C–C stretching vibrations occurs in the region 1000-1300 cm-1 [49]. The C-H in-plane bending vibrations were predicted at 1310.92, 1362.42, 1392.24, 1423.32, 1476.84 cm-1 and the corresponding modes were observed as strong peaks at 1348, 1368, 1391, 1400, 1461 cm-1 in Fourier Transform Infrared (FTIR) spectroscopy and in Raman at 0.7304, 68.0035, 47.435, 25.6914, 4.5186 cm-1.
The CH out-of-plane bending vibrations appear in the region 1050-700 cm-1 [46]. Accordingly, The FTIR bands observed as weak to strong peaks at 690.19, 853.96, 891.45 and 956.62 cm-1 are assigned to C-H out-of-plane bending vibrations, which are in good agreement with the experimental values 777, 822, 882 and 1015 cm-1 at 0.4071, 1.0029, 0.2556 and 0.2301 cm-1 in the Raman spectrum.
C=N, C-N vibrations
The identification of the C–N stretching frequency in the side chains is a rather difficult task since there are problems in identifying these frequencies from other vibrations [50]. In the present study, the ring C-N stretching vibrational modes occur in the region 1600-1080 cm-1 where the weak to strong intense bands observed at 1109, 1158, 1573, 1580 cm-1 in FTIR and the bands at 12.8276, 0.6055, 5.1509, 2.8246 cm-1 in Raman are allotted to C-N, C=N stretching vibration. The observed results are well matching with calculated values.
C=C Vibrations
The aromatic ring C=C stretching vibrations usually present in the region 1635-1080 cm-1 [48]. In the present study, the bands were of variable intensity and were found at 1092, 1286, 1368, 1435, 1558 cm-1 in FT-IR which are assigned to C-C stretching vibrations in pteridine. The same vibrations were observed in Raman at 3.9258, 11.8581, 68.0035, 0.2466 and 39.9912 cm-1. The calculated values at 1048.04, 1300.82, 1362.42, 1457.74 and 1542.08 cm-1, respectively, these assignments are in quite agreement with experimental data.
Ring Vibrations
Generally, ring vibrational modes are quite sensitive to substitution [51-54] where the bands were found at 1048.04, 1090.91, 1181.19, 1300.82, 1457.74, 1542.08, 1575.12 and 1592.98 cm-1 in FTIR. These bands are attributed to ring in plane bending modes, while experimentally found modes were found at 1092, 1109, 1158, 1286, 1435, 1558, 1573 and 1580 cm-1, whereas in Raman were found at 3.9258, 12.8276, 0.6055, 11.8581, 0.2466, 39.9912, 5.1509 and 2.8246 cm-1.
The ring out-of-plane bending mode frequencies were at 195.07 cm-1 and in Raman at 0.4515 cm-1, while no vibration was identified in experimental data.
The bands at 933, 455 cm-1 in the infrared and 0.3971, 0.3362, 0.1543 cm-1 in Raman were assigned to the N-C-H in plane bending vibrations and C-C-H/N-C-H out plane bending vibrations, respectively, whereas the same bands were calculated at 951.55, 478.63, 159.76 cm-1. In addition to these bending vibrations, C-N-C, C-C-N and N-C-N bending vibrations were assigned in the characteristic range in pteridine molecule.
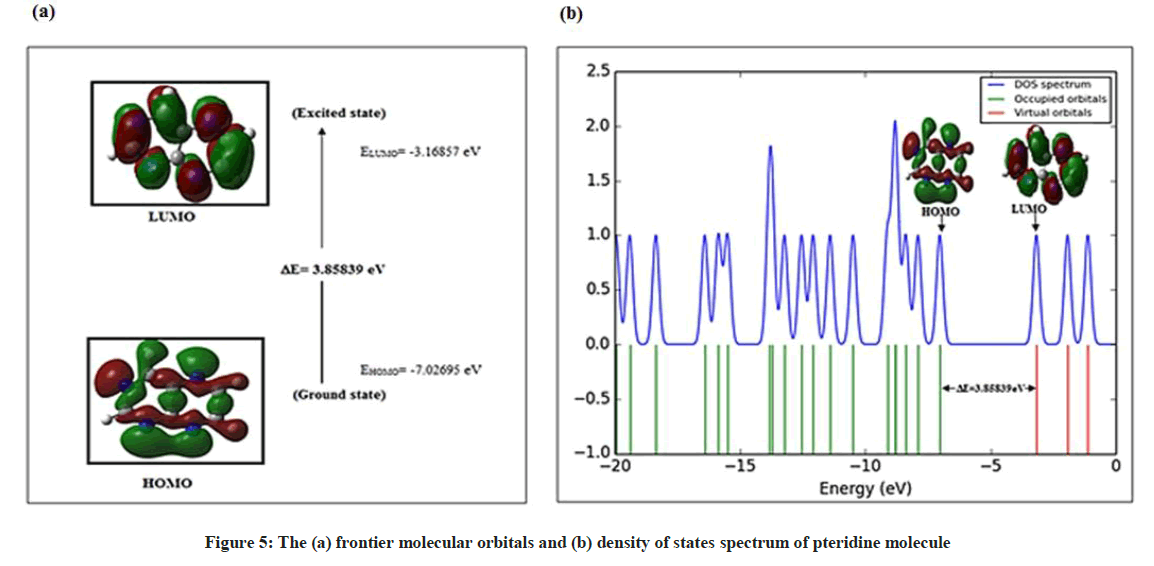
Frontier Molecular Orbitals (FMOs) analysis
The highest occupied molecular orbital (HOMO) represents the outermost orbital filled by electrons and behaves as an electron donor, while the lowest unoccupied molecular orbital (LUMO) considers as the first empty innermost orbital unfilled by electron and behaves as an electron acceptor [55]. These orbitals are also called as frontier molecule orbital (FMOs) which analysis predicts the molecular interactions with other species and has great importance in modern biochemistry and molecular biology [56]. According to B3LYP/6–311G calculation, The energy gap between HOMO and LUMO is -3.85839 eV which indicates the molecular chemical stability and it is a critical parameter to determine molecular electrical transport properties [55]. The calculate ionization energy and electron affinity can express through HOMO and LUMO orbitals energies as I= -EHOMO and A = -ELUMO. The term ‘η’ has come to be used to refer to the global hardness, η =½(ELUMO - EHOMO), the hardness has been associated with the stability of chemical system. The electron affinity can be used in combination with ionization energy to give electronic chemical potential, μ= ½(ELUMO + EHOMO). The term ‘ω’ refer to the global electrophilicity index, 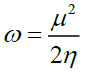 [57]. Electronegativity,
[57]. Electronegativity,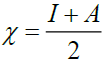 , is the tendency of an atom to attract electrons. The term ‘S’ is generally understood to mean the chemical softness,
, is the tendency of an atom to attract electrons. The term ‘S’ is generally understood to mean the chemical softness, 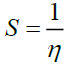 [58]. These values of Electronic structure parameters are given in Table 3.
[58]. These values of Electronic structure parameters are given in Table 3.
| Molecularproperties | Energy |
|---|---|
| EHOMO(eV) | -7.02695 |
| ELUMO(eV) | -3.16857 |
| Energie gap (EHoMO -ELuMO)(eV) | -3.85839 |
| Ionizationenergy (eV) | 7.02695 |
| Electron affinity (eV) | 3.16857 |
| Global hardness (eV) | 1.92933 |
| Chemical potential (eV) | -5.0979 |
| Electrophilicity index (eV) | 6.73523 |
| Electronegativity (eV) | 5.0979 |
| Softness (eV-1) | 0.51831 |
Table 3: Electronic structure parameters of the title compound
The Gauss Sum program was used to obtain the density of states DOS diagram which was convoluted from the molecular orbital data as shown in Figure 5.
Local reactivity descriptors and molecular electrostatic potential
The local reactivity descriptors such as Fukui functions (fk+, fk−, fk0) were calculated at the B3LYP/6–311G for the pteridine molecule using Natural Bond Orbital (NBO) analysis to predict the possible reactive sites of the molecule where a chemical species will change its density when the number of electrons is modified Thus, the propensity of the electronic density to deform at a given position upon accepting or donating electrons. Itis an important in designing a pharmaceutical compound [59-62]. The corresponding condensed or atomic Fukui functions (FF) can be evaluated through the following equations [63]:
f k+ = qk(N +1) − qk(N) for nucleophilic attack
f k− = qk(N) − qk(N −1) for electrophilic attack
f ko= [qk(N + 1) − qk(N −1)] /2 for radical attack
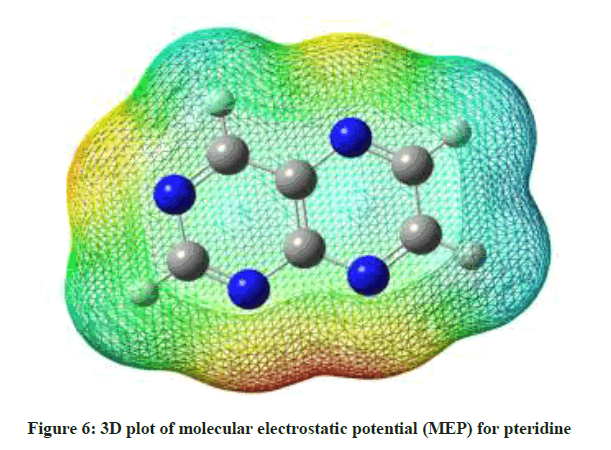
and the importance of MEP, it displays molecular size, shape as well as positive, negative and neutral electrostatic potential regions in terms of color grading red < orange < yellow < green < blue. Where red, blue and green represent the regions of most negative, most positive and zero electrostatic potential respectively [64-66]. As depicted in (Figure 6), regions of negative potential are over the nitrogen atoms and the regions having the positive potential are over the hydrogen atoms.
On the other hand, It was noted in Table 4 that the highest value of fukui functions for the LUMO (fk+=0.1900) present around N (1), which indicates electrophilic site and hence possible site for nucleophilic attacks. The highest of fukui functions for the HOMO (fk-=0.1410) present around N (5) and N (8), which indicate nucleophilic site and these are the possible sites for electrophilic attacks. While, the atom N (1) characterized by the highest value of fk0 (fk0=0.1500) indicates that this atom is the most important site for radical attacks.
| B3LYP/6-311G | ||||||
|---|---|---|---|---|---|---|
| Atom | P (N) | P (N+1) | P (N-1) | fk+ | fk- | fk0 |
| 1N | -0.424 | -0.234 | -0.534 | 0.19 | 0.11 | 0.15 |
| 2C | 0.26 | 0.3 | 0.208 | 0.04 | 0.052 | 0.046 |
| 3N | -0.449 | -0.304 | -0.538 | 0.145 | 0.089 | 0.117 |
| 4C | 0.113 | 0.143 | -0.017 | 0.03 | 0.13 | 0.08 |
| 5N | -0.385 | -0.256 | -0.526 | 0.129 | 0.141 | 0.135 |
| 6C | 0.026 | 0.078 | -0.055 | 0.052 | 0.081 | 0.0665 |
| 7C | 0.038 | 0.089 | -0.069 | 0.051 | 0.107 | 0.079 |
| 8N | -0.374 | -0.273 | -0.515 | 0.101 | 0.141 | 0.121 |
| 9C | 0.325 | 0.329 | 0.338 | 0.004 | -0.013 | -0.0045 |
| 10C | 0.054 | 0.099 | 0.056 | 0.045 | -0.002 | 0.0215 |
| 11H | 0.196 | 0.247 | 0.153 | 0.051 | 0.043 | 0.047 |
| 12H | 0.212 | 0.271 | 0.174 | 0.059 | 0.038 | 0.0485 |
| 13H | 0.204 | 0.254 | 0.163 | 0.05 | 0.041 | 0.0455 |
| 14H | 0.204 | 0.257 | 0.163 | 0.053 | 0.041 | 0.047 |
Table 4: Values of the condensed Fukui function in pteridine computed from NBO charges
Conclusion
The present study deals with the comparison between the calculated and experimental structural parameters indicate that B3LYP/6–311G is in good agreement with experimental observations. In addition, theoretically calculated and experimentally observed vibrational wavenumbers were compared and assigned on the same level of calculations. Our work was mainly based on the study of both reactivity and selectivity also oriented towards the search for the most stable molecular conformation and which are largely responsible for binding of small molecule to its active site. Thus, at the B3LYP/6-311G level, which provide the nature of reactivity, the energies of HOMO/LUMO and their orbital energy gaps were calculated as well as electronic structure parameters of the molecules. Fukui function with NBO charge was positive value around N (1) at places which are better at accepting electron than they are at donating electrons. Conversely, zones with negative values around N (5) and N (8) which means that these sites donate electrons rather than accept electrons.
References
- L.A. Thompson, J.A. Ellman, Chem. Rev., 1996, 96(1), 555-600.
- F.G. Hopkins, Philosophical Transactions of the Royal Society of London B, 1895, 186, 661-682.
- C. Schöpf, H. Wieland, Eur. J. Inorg. Chem., 1926, 59(8), 2067-2072.
- W. Koschara, Hoppe-Seyler´s, J. Physiol. Chem., 1936, 240(3-4), 127-151.
- I. Ziegler, R. Harmsen, Adv. ins. Physiol., 1969, 6, 139-203.
- W. Pfleiderer, R.A.L. Levine, Unconjugated pterins in neurobiology, Taylor & Francis: London, 1987.
- W. Pfleiderer, Comprehensive Heterocyclic Chemistry II, AR Katritzky, CW Rees, EF Scriven, (Eds.), Pergamon, Oxford, 1996, 7, 679-736.
- I.M. Kompis, K. Islam, R.L. Then, Chemi. Rev., 2005, 105(2), 593-620.
- P.W. Ayers, J.S. Anderson, L.J. Bartolotti, Int. J. Quantum Chem., 2005, 101(5), 520.
- H. Chermette, J. Comput. Chem., 1999, 20(1), 129.
- P. Geerlings, F. De Proft, W. Langenaeker, Chemi. Rev., 2003, 103(5), 1793-1873
- R.G. Parr, W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
- M. Mellaoui, S. Belaidi, D. Bouzidi, N. Gherraf, Quantum Matter., 2014, 3(5), 435-441.
- S. Belaidi, H. Belaidi, D. Bouzidi, J. Comput. Theor. Nanosci., 2015, 12(8), 1737.
- E. Davidson, Chem. Rev., 1991, 91(5), 649.
- N. Melkemi, S. Belaidi, J. Comput. Theor. Nanosci., 2014, 11(3), 801.
- F. Billes, H. Mikosch, S. Holly, J. Mol. Struc.: THEOCHEM., 1998, 423(3), 225-234.
- A.J. Blake, D.W. Rankin, Acta Crystallographica Section C: Crystal Struc. Commun., 1991, 47(9), 1933-1936.
- S. Cradock, C. Purves, D.W. Rankin, J. Mol. Struc., 1990, 220, 193-204.
- M. Govindarajan, K. Ganasan, S. Periandy, M. Karabacak, Spectrochim. Acta Part A: Mol. Biomol. Spectro., 2011, 79(3), 646-653.
- D. Holland, L. Karlsson, W. Von Niessen, J. Electron Spectro. Rel. Phenomena., 2001, 113(2), 221-239.
- M. Karabacak, M. Cinar, M. Kurt, J. Mol. Struc., 2010, 968(1), 108-114.
- M. Karabacak, M. Cinar, Z. Unal, M. Kurt, J. Mol. Struc., 2010, 982(1), 22-27.
- M. Karabacak, M. Kurt, A. Atac, J. Phys. Org. Chem., 2009, 22(4), 321-330.
- M. Karabacak, E. Şahin, M. Çınar, I. Erol, M. Kurt, J. Mol. Struc., 2008, 886(1), 148-157.
- M. Kurt, T.R. Sertbakan, M. Özduran, M. Karabacak, J. Mol. Struc., 2009, 921(1), 178-187.
- A. Navarro, M.F. Gómez, J.J.L. Gonzaléz, M.P.F. Liencres, E.M. Martinez Torres, J.T.G.I. Kearley, J. Phys. Chem. A, 1999, 103, 5833-5845.
- A. Potts, D. Holland, A. Trofimov, J. Schirmer, L. Karlsson, K. Siegbahn, J. Phys. B: Atomic, Mol. Opt. Phys., 2003, 36(14), 3129.
- Y.I. Suzuki, T. Suzuki, J. Phys. Chem. A, 2008, 112(3), 402-411.
- S. Belaidi, L. Bouchlaleg, D. Harkati, T. Salah, J. Pharm. Biol. Chem. Sci., 2015, 6(2), 861-873.
- H. Buyukuslu, M. Akdogan, G. Yildirim, C. Parlak, Spectrochim. Acta Part A: Mol. Biomol. Spectro., 2010, 75(4), 1362-1369.
- H. Elhaes, A. Babaier, J. Comput. Theor. Nanosci., 2011, 8(8), 1509-1512.
- Hyper Chem, (Molecular modeling system) Hypercube, Inc., 1115NW, 4th Street, Gainesville, FL 32601, USA, 2007.
- M. Frisch, G. Trucks, H.B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. Petersson, H.C.M. Nakatsuji, X. Li, H.P.I.A.F. Hratchian, J. Bloino, G.S.J.L. Zheng, M.E.M. Hada, K. Toyota, R.H.J. Fukuda, M.N.T. Ishida, Y.K.O. Honda, H. Nakai, T. Vreven, J.A.Jr. Montgomery, J.E. Peralta, F.B.M. Ogliaro, J.J.B.E. Heyd, K.N.S.V.N. Kudin, R.N.J. Kobayashi, K.R.A. Raghavachari, J.C.I.S.S. Burant, J.C.M. Tomasi, N. Rega, N.J.K.M. Millam, J.E.C.J.B. Knox, V. Bakken, C.J.J. Adamo, R. Gomperts, R.E.Y.O. Stratmann, A.J.C.R. Austin, C.O.J.W. Pomelli, R.L.M.K. Martin, V.G.V.G.A. Zakrzewski, P.D.J.J. Salvador, S.D.A.D. Dapprich, Ö.F.J.B. Farkas, J.V.C.J. Ortiz, D.J. Fox, Gaussian, Inc., Wallingford, CT, 2009.
- A.D. Becke, J. chem. Phy., 1993, 98 (7), 5648-5652.
- C. Lee, W. Yang, R.G. Parr, Physical review B., 1998, 37, 785-789.
- Marvin Sketch, 6.2.1; Chemaxon (http://www.chemaxon.com), 2014.
- R. Dennington, T. Keith, J. Millam, Semichem. Inc., Shawnee Mission, KS, 2009.
- M.D. Hanwell, D.E. Curtis, D.C. Lonie, T. Vandermeersch, E. Zurek, G.R. Hutchison, J. chem. Inform., 2012, 4(1), 17.
- N.M. O'boyle, A.L. Tenderholt, K.M. Langner, J. comput. Chem., 2008, 29(5), 839-845.
- J.E. Gready, J. Mol. Struc.: THEOCHEM., 1985, 124(1-2), 1-8.
- F. Weinhold, C.R. Landis, Chemistry Education Research and Practice, 2001, 2(2), 91-104.
- F. Weinhold, C.R. Landis, Valency and bonding: a natural bond orbital donor-acceptor perspective, Cambridge University Press, 2005.
- R.G. Parr, In Horizons of Quantum Chemistry: Proceedings of the Third International Congress of Quantum Chemistry Held at Kyoto, Japan, October 29 - November 3, 1979, K. Fukui, B. Pullman, (Eds.), Springer Netherlands, Dordrecht, 1980, 5-15.
- C.D. Sherrill, J. chem. Phys., 2010, 132(11), 110902.
- S. Mason, J. chem. Phys., 1955, 2336-2346.
- G. Socrates, John Wiley & Sonsohn, Ltd., New York, 2001.
- G. Varsányi, Assignments for vibrational spectra of 700 benzene derivatives, Adam Hilger, London, 1974.
- A. Srivastava, V. Singh, Indian J. Pure Appl. Phys., 2007, 45, 714-720.
- S. Pinchas, D. Samuel, M. Weiss-Broday, J. Chem. Soc., (Resumed) 1961, 1688-1692.
- R. Jakobsen, F. Bentley, Appl. Spectro., 1964, 18.
- A. Mansingh, J. Chem. Phys., 1970, 52(11), 5896-5901.
- L. Verdonck, G. Van der Kelen, Z. Eeckhaut, Spectrochim. Acta Part A: Mol. Spectro., 1973, 29(5), 813-816.
- L. Verdonok, G. Van Der Kelen, Spectrochim. Acta Part A: Mol. Spectro., 1972, 28(1), 51-54.
- K. Fukui, Science., 1982, 218(4574), 747-754.
- S. Premkumar, T. Rekha, R.M. Asath, T. Mathavan, A.M.F. Benial, Eur. J. Pharm. Sci., 2016, 82, 115-125.
- P.M. Anbarasan, P.S. Kumar, K. Vasudevan, R. Govindan, A. Prakasam, M. Geetha, Eur. J. Chem., 2011, 2(2), 206-213.
- R.G. Pearson, Proceedings of the National Academy of Sciences, 1986, 83(22), 8440-8441.
- P.W. Ayers, R.G. Parr, J. Am. Chem. Soc., 2000, 122(9), 2010-2018.
- K. Fukui, Springer-Verlag, Berlin, 1975.
- R. Parr, W. Yang, J. Am. Chem. Soc., 1984, 106(14), 4049-4050.
- R. Parr, W. Yang, Oxford University Press, New York, 1989.
- R. Parr, W. Yang, Density-Functional Theory of Atoms and Molecules, 1st (Edn.), Oxford University Press, New York, 1989.
- J. Šponer, P. Hobza, Int. j. quantum chem., 1996, 57(5), 959-970.
- E. Scrocco, J. Tomasi, Advances in quantum chemistry, Academic Press, New York, 1978, 11, 115-193.
- J.S. Murray, K. Sen, Molecular electrostatic potentials: concepts and 399 applications, Elsevier, Amsterdam, 1996.