Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 8
Molecules: Application on N-Formyl-Glycine-L-Tyrosine-Glycine N-Amide Tripeptide Model
Anouar El Guerdaoui* and Abderrahman El Gridani
Team of Theoretical Chemistry, Electrochemistry and Environment CT2E, Faculty of Sciences, Ibn Zohr University, B.P. 8106, Agadir, Morocco
- *Corresponding Author:
- Anouar El Guerdaoui
Team of Theoretical Chemistry
Electrochemistry and Environment CT2E
Faculty of Sciences, Ibn Zohr University
B.P. 8106, Agadir, Morocco
Abstract
The conformational landscape of the tripeptide Gly-L-Tyr-Gly with protected N- and C- termini has been explored by using a genetic algorithm combined with DFT and MP2 calculations in order to investigate all potential minima on its potential energy surface (PES). The genetic algorithm based on the Multi-Niche Crowding (MNC) technique was used to generate a set of most probable equilibrium structures for the title compound. Resulting structures will then be submitted to an hierarchy of increasingly more accurate electronic structure calculations (single-point HF/3-21G* energy calculation, HF/6-31+G(d) geometry optimization, B3LYP/6-311++G(2d,2p) geometry optimization and MP2/6-311++G(2d,2p) single-point energy calculation). The developed procedure was tested by comparing the obtained results (stabilities, geometrical parameters and relative energies of localized conformers) with those derived from a commonly used ordinary optimization strategy. Our method was able to predicted 18 conformations among 28 localized by the ordinary strategy and in which the 11 most stables ones are in the same stability order. The comparison of 18 common conformation geometries revealed nearly perfect linear adjustments with R2 values of 0.9996, 0.9992, 0.9988, and 0.9988 for dihedral angles φtyr, ψtyr, χ1 and χ2 respectively. Relative energies of the matching 18 conformers also fitted to a linear plot with an R2 value of 0.9962.
Keywords
Genetic algorithm, DFT calculations, Potential energy surface, Tripeptide.
Introduction
In the activities associated with biological evolution, the recent revolution in genomics has forced scientists, biologists and chemists, to extend their field of investigation to the relationship between sequences-structures-functions for both cognitive and economic reasons; current bioinformatics approaches (archiving, data mining, sequence analysis, etc…) can only trace the function of a protein through its three-dimensional structure [1]; these structures are determined by the spectroscopic analysis methods; include X-rays crystallography, NMR, UV-UV and IR-UV hole burning spectroscopies. However, the identification of these experimentally detected structures requires comparison with computed data from quantum calculations on the energetics and vibrational frequencies in order to convert the observed spectra into structural assignments, which requires the exploration of their conformational spaces by the quantum calculation tools, including semi-empirical methods that can treat molecules of considerable size, and therefore allow a good exploration of their conformational spaces. However, these methods are less rigorous since their mathematical basis is based on a multitude of approximations which does not allow the proper description of the intermolecular interactions within these structures. On the other hand, correlated methods, like density functional theory DFT and Møller-Plesset perturbation theory up to second order MP2 which take into account part of the electronic correlation for example, are widely used to model simple organic or bio-organic molecules and are expected to describe electric moments and polarizabilities [2] accurately and are known to give reasonable description of hydrogen-bonding energies [3]. However, identifying the equilibrium structure by investigating all possible conformations at these high levels of the theory quickly becomes an expensive task for peptides consisting of more than two or three amino acid residues [4,5]. The flexible character of amino acids and therefore their peptides, due mainly to the possible rotations around the numerous simple bonds which constitute them present a major problem to be integrated. The number of possible conformations increases dramatically with the size of the molecule, this number of conformers is function of the (n) dihedral angles to be varied and the step of increment used. For example, it is equal to 12n if each angle is varied between -180° and +180° in steps of 30°. These constraints related to the exploration of the conformational space of large molecules size have not prevented theoretical chemists and computer scientists to develop other techniques of conformational research which can (a) treat large molecular systems, (b) offer comparable results to the experience with (c) a reasonable calculation time. In this sense, a new mathematical optimization road knows a growing development. The stochastic methods such as simulated annealing [6] and genetic algorithms [7,8], gradually take precedence over the conventional deterministic techniques. On the one hand, they help in locating the optimum of a function in the parameters’ space without using the derivatives of the function with respect to these parameters, on the other hand, they do not get trapped by a local optimum and usually manage to determine the global optimum of the function in question. Our ultimate goal in this paper is to develop a practical that allows exploration of the conformational space of bio-molecules which present a major challenge at correlated and DFT levels of theory; it's about a genetic algorithm whose parameterization is improved in such a way as to make it suitable to seek multiple potential solutions simultaneously to an optimization problem, instead of seeking only one optimal solution (global minimum), which is relevant with our desired objective to locate all possible minima of a biomolecular-system. In this work, the conformational landscape of Gly-L-Tyr-Gly-NH2 tripeptide model was explored by using a genetic algorithm based on the MNC technique [9] combined with the most popular electronic structure methods, DFT and MP2, used in computational chemistry studies on organic molecules. We will discuss the effectiveness of the used procedure to predict the equilibrium structures (global minimum and local minima) of the title compound. This will give us a promising opportunity to efficiently process other types of biological-compounds, especially those present complicated PESs such as peptide chains.
Materials and Methods
Conformational and mathematical definitions
Conformational details
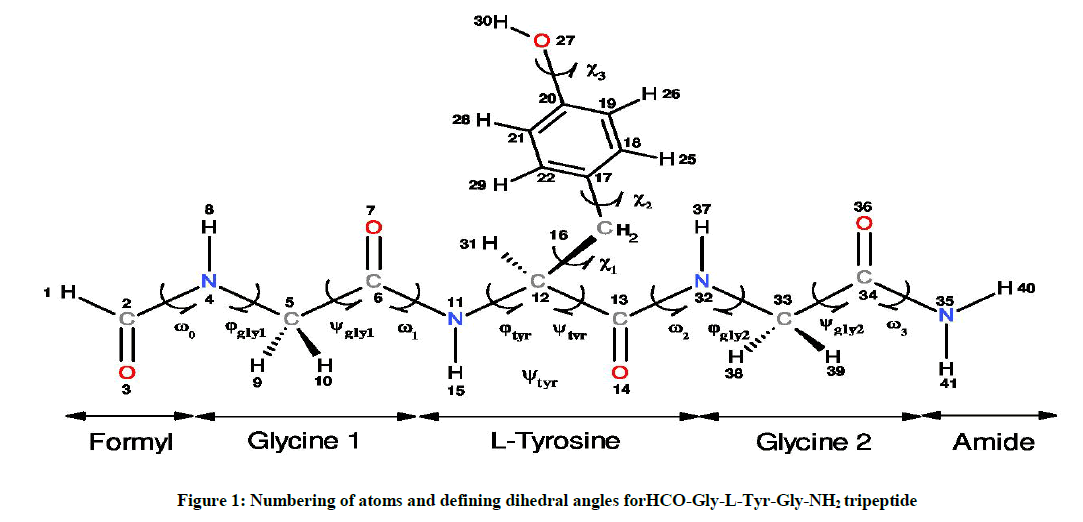
As illustrated in Figure 1, the formyl (HC=O) and the -amide (-NH2) groups were used as protecting end groups to mimic the steric effects of the neighboring amino acid residues on the tripeptide motif Glycine-L-Tyrosine-Glycine (Gly-L-Tyr-Gly) as they can occur in proteins [10]. This approach which aims to protect amino acids (and peptide) by formyl (or acetyl) and amide groups [11,12], has been widely used in recent years to model a wide range of naturally occurring amino acids [13-18] and their peptides respectively [19].
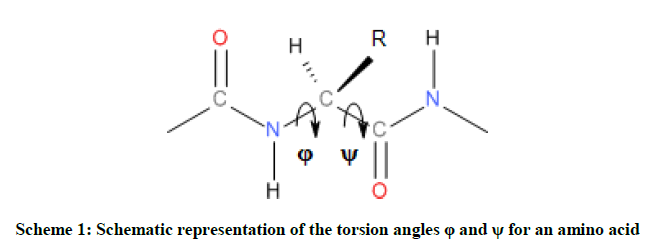
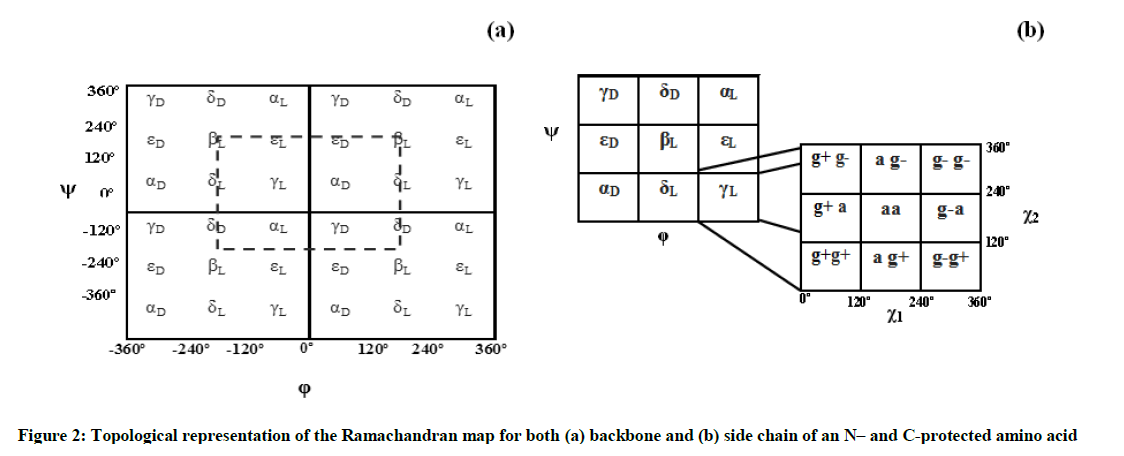
Otherwise, the spatial arrangements of an amino acid are resulted from variation of dihedral angles φ and ψ as shown in Scheme 1, and they are associated to specifically notation given by the multi-dimensional conformational analysis MDCA rules [20]. These rules predicted the existence of 9 possible conformations for the backbone of any amino acid (Figure 2a). These 9 conformations marked by greek letters attached to the two letters L or D (αD αL, γD, γL, βL, δD, δL, εD and εL) are often represented on a map called Ramachandran map E = f (φ,ψ) as illustrated in Figure 2a.
In the current study, the Backbone of the HCO-Gly-L-Tyr-Gly-NH2 peptide model has ten torsion angles noted as follow: ω0, φgly1, ψgly1, ω1, φtyr, ψtyr, ω2, φgly2, ψgly2, ω3 and represent the rotations around the bonds C2-N4, N4-C5, C5-C6, C6-N11, N11-C12, C12-C13, C13-N32, N32-C33, C33-C34 and C34-N35 respectively as shown in Figure 1. A statistical study on the dihedral angles ω of amino acid residues, collected from non-homologous proteins e tracted from the "Protein Data Bank" PDB [21] shows that the dihedral angles ω ta e average values around 179.5° ± 3.8°. In this work, and li e other studies found in the literature, the dihedral angles, associated with the peptide bonds (ω0, ω1, ω2 and ω3) have a value of 180º and corresponding consequently to trans-peptide (where ω≈ 180º).
Glycine amino acid occupies very little space and thus allows different polypeptide strands to easily come together in restricted spaces. Glycine is known as the simplest amino acid due to its side chain consisting of only an H atom, however, in protein structure, this simplicity is of great significance [22]. Thus, the side chain of the studied HCO-Gly-L-Tyr-Gly-NH2 peptide model, which obviously corresponds to that of L-tyrosine residue, is defined by the three angles of χ1, χ2 and χ3 (Figure 1) whose both dihedral angles χ1 and χ2 can take three possible orientations, gauche + (g+= +60º), anti (a=180º) and gauche - (g- =-60º) leading in total to 3 × 3=9 possible orientations for this chain as illustrated in Figure 2b Torsional angle χ3 may take in general the two positions Cys (s) and trans (a) corresponding to the values 0° and 180° respectively. Limiting our considerations only for χ3 =180°, this leads in total to 9 × 9=81 possible conformations for L-Tyr residue. On the other side, the two terminal glycine residues of the considered tripeptide were chosen at a time to be in the fully e tended βL form (φ= 80°; ψ= 80°), in order to monitor their effects on the L-Tyr residue with varying the backbone conformation. Studies conducted on the protected amino acid HCO-Glycine-NH2 [7] as well as Ac-Glycine-NH2 (Ac=acetyl) [19] have shown both conformations βL and γL are the most stable for this residue, these backbones do not migrate to another catchment region during their optimization, what justifies our choice to limit our study to one of these two folds which consequently leads to 81 possible conformations for the studied tripeptide as described in Scheme 2 (see reference [15] for more explanation). The term migration is used here when a folding type (either of the backbone or of the side chain) of the optimized conformer is different from that of its input.
In accordance with the IUPAC-IUB recommendation [23], torsional angles were varying [24] between - 80° and 80° for both bac bone (φ,ψ) and side chain (χ1,χ2) conformations (Figure 2).
Computational detail
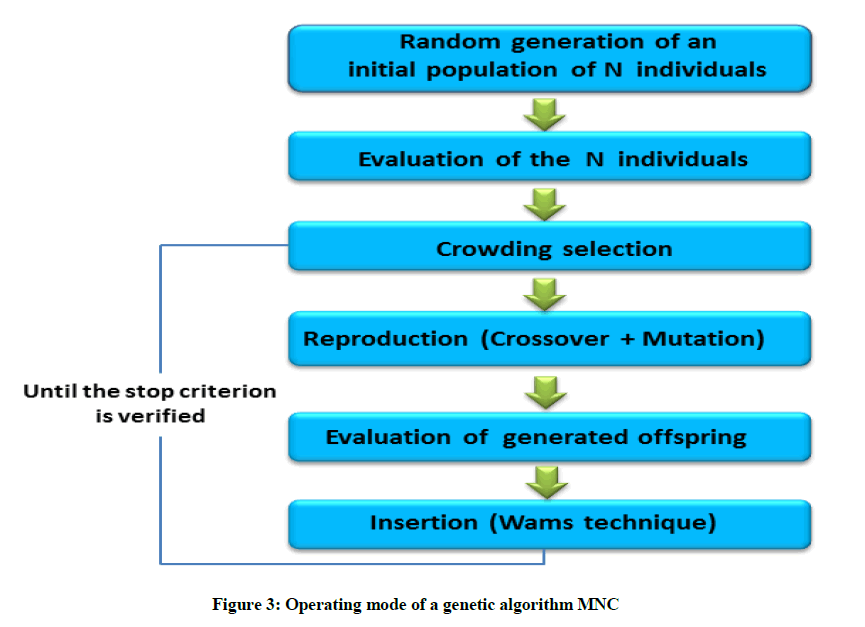
The conformational landscape of the neutral gas-phase HCO-Gly-L-Tyr-Gly-HN2 tripeptide model was explored initially by using a genetic algorithm based on the Multi-Niche Crowding (MNC) technique, developed recently, to explore potential energy surfaces of biological molecules [25] and tested on a set of protected aromatic amino acids [26,27]. The MNC genetic algorithm is implemented in a package of program interfaced with MOPAC (version 6.0) [28]. The semi-empirical method AM1 is used to calculate the energy of each molecule (the heat of formation in our case) generated by application of the genetic parameters (crossover and mutation) [25]. In the case of genetic algorithms, two constraints must be taken into consideration for an efficient space exploration of the molecular systems: the first is to minimize the calculation time and second is to limit the risk of missing the global minimum which represents the most likely equilibrium structure. Regarding the time of calculation, it depends on the number of individuals (molecular-conformations in our case) in the first population generated randomly by the genetic algorithm. Indeed, more of individuals in the population, will therefore require the application of these operators several times, and by consequence the calculation time will increase. As to the problem of locating the global minimum, more the size of the population is important, more we will have chances to well explore the space of the solutions [29]. It is quite obvious that a molecular system with a large number of degrees of freedom (dihedral angles) will require a large population for a better exploration of its conformational space, which in many cases justifies the role of a large population size. Since the size of the molecular system treated in this work is relatively large, we will work on a population of 1000 conformations than that previously chosen (500 conformations) for the HCO-L-Tryptophan-NH2 [26] and HCO-L-Tyrosine-NH2 [27], that have moderate sizes system. The 1000 conformations of the first population are generated randomly. Once the algorithm converges after a fixed number of generations (100 generations), an optimization without constraint is performed in order to release the structure so that the individuals (structures) of the same niche converge to the corresponding minimum. The exploration of the potential energy surface of the HCO-Gly-L-Tyr-Gly-NH2 tripeptide is conducted according to its promising and productive areas. The result is an algorithm that (a) maintains stable subpopulations within different niches, (b) maintains diversity throughout the search, and (c) converges to different minima. Figure 3 presents a simplified diagram of the operating mode of a genetic algorithm based on the MNC technique.
This preliminary PES scan allowed us to generate a set of 1000 probable equilibrium structures for HCO-Gly-L-Tyr-Gly-NH2 system. These were then submitted to HF/3-21G* single point energy calculations. The first 200 most stable conformers based on HF/3-21G* single-point energy were subjected to full geometry optimization at HF/6-31G+(d) level of theory. Some conformers exhibit significant steric clashes and are therefore eliminated, which reduced the number of resulting structures to 168. The 50 most possible structures obtained from these calculations were subjected to further geometry optimization by applying density functional theory (DFT) and using the Becke3-Lee-Yang-Parr functional [30,31] with 6-311++G(2d,2p) basis set (B3LYP/6-311++G(2d,2p)), leading to 48 unique conformations. The harmonic vibrational frequencies were calculated for the 48 localized conformers through the DFT level of theory and no imaginary frequencies were observed, which shows that they are true minima. It's worth noting that at this stage of calculations, geometry optimization of the studied tripeptide using the large-sized basis set 6-311++G(2d,2p) can offer more reliable structures; previous study carried out by Van-mourik et al. [32] on the tyrosine-glycine dipeptide have shown that 6-311++G(2d,2p) basis set predicts less Basis set Superposition Error (BSSE) [33] effect, which is an artificial (unphysical) interaction that can arise in a superamolecular system with respect to isolated compounds (monomers) that composing it, compared with 6-31+G(d) at both DFT and MP2 levels of theory. In weakly bound complexes or dimers [34-36] this unphysical effect occurs when a monomer of the considered superamolecular system use basis functions from its partners (other monomers) improving its basis set and therefore its energy. BSSE can also affect single molecules (intramolecular BSSE). In this case, a part of a molecule may be stabilized by using basis functions from other parts of the same molecule. Additionally, relative energies of the 20 most stable conformers resulting from the B3LYP/6-311++G(2d,2p) geometry optimization were evaluated by single-point calculations at MP2/6-311++G(2d,2p) level of theory including evaluation of zero-point energies (ZPEs) calculated at DFT/B3LYP/6-311++G(2d,2p). The main idea behind the use of this hierarchical optimization scheme (HF, DFT and MP2 geometry and energy optimizations) is that energy of a molecule is generally more sensitive to the used level of theory than to its adopted geometry. Therefore, it is more practical to optimize geometries with DFT functionals and then evaluate the energies at more accurate level of theory such as MP2. All calculations were performed using the Gaussian09 program [37] and MOPAC software package (version 6.0) [28]. Relative energies are given in kilocalories per mole (using the conversion factor: 1 hartree=627.5095 kcal mol-1).
Results and Discussion
Conformational space exploration by using the genetic algorithm MNC combined with the electronic structure calculations
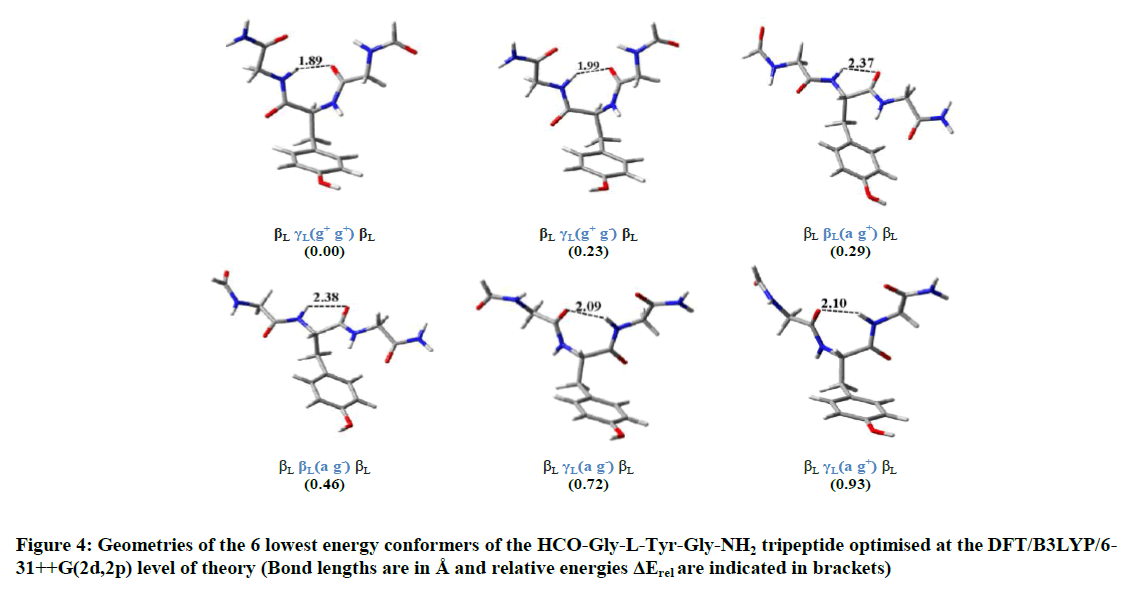
Results of geometry optimizations of the 20 most stable DFT/B3LYP/6-311++G(2d,2p) conformers (based on single-point MP2 energies corrected by B3LYP zero-point energies) including geometrical parameters (dihedral angles) and relative energies evaluated at the MP2/6-311++G(2d,2p) level of theory are given in Table 1.
| Backbone Conformation | Glycine (1) (βL) | Tyrosine | Glycine (2) (βL) | ΔErel (in Kcal.mol-1) at MP2/ 6-311++G (2d,2p) (b) | |||||
|---|---|---|---|---|---|---|---|---|---|
| φ1 | ψ1 | φtyr | ψyr | χ1 | χ2 | φ2 | ψ2 | ||
| βLγL (g+ g+)βL | -157.8 | -167.4 | -79.4 | 61.1 | 50.2 | 81.1 | 147.3 | -167.8 | 0 |
| βLγL (g+ g-)βL | -141.9 | -157.1 | -83.2 | 59.4 | 48.4 | -111.8 | 143.9 | -165.2 | 0.23 |
| βLβL (a g+)βL | 153.8 | 165.8 | -159.1 | 151.8 | -163 | 78.8 | -121.9 | 162.6 | 0.29 |
| βLβL (a g-)βL | 179.8 | -145.9 | -161.4 | 162.9 | -158.6 | -109.3 | -149.1 | 167.3 | 0.46 |
| βLγL (a g-)βL | -157.2 | 139.3 | -79.9 | 74.2 | -157.2 | -89.6 | -147.9 | 155.2 | 0.72 |
| βLγL (a g+)βL | 148.6 | 153.5 | -80 | 74.5 | -152.9 | 87.2 | -147.4 | 158.1 | 0.93 |
| βLγL (g- g-)βL | 157.1 | -149.1 | -80.4 | 72.9 | -56.3 | -71.6 | 146.6 | 168.5 | 1.02 |
| βLγL (g- g+)βL | 156.7 | -143.6 | -80.2 | 71.7 | -50.4 | 110 | -146.9 | 161.8 | 1.06 |
| βLγD (g- g+)βL | 157. 1 | -147.4 | 71.9 | -59.4 | -60.8 | 98.9 | 143 | -156.8 | 1.88 |
| βLγD (g- g-)βL | 157.4 | 141 | 70.4 | -59.2 | -59.9 | -76.7 | -141.5 | 148.1 | 1.97 |
| βLβL (g+g+)βL | -156.6 | -147.1 | -150.9 | 173.7 | 61.3 | 82.1 | 146.6 | 157.6 | 2.09 |
| βLβL (g- g-)βL | -158.3 | -146.5 | -129.1 | 139.3 | -63.4 | -80.5 | 148.7 | 158.1 | 2.61 |
| βLαL (g- g-)βL | -158.2 | -142.3 | -74.8 | -18 | -63.9 | -70.4 | 141.6 | 154.7 | 2.71 |
| βLγD (a g-)βL | 157.8 | 148.2 | 69.8 | -67.9 | -161.4 | -90.8 | -147.3 | 157.5 | 3.65 |
| βLγD (a g+)βL | -156.2 | 157.2 | 70.1 | -66.4 | -169.3 | 78.1 | 169.9 | 158.1 | 3.78 |
| βLδD (g+ g-)βL | -158.2 | 158.5 | -169.4 | -38.3 | 51.6 | -84.8 | 147.1 | 157.5 | 5.65 |
| βLδD (g+ g+)βL | 159.4 | -151 | -172.5 | -29.4 | 54.1 | 89.2 | -156.4 | 158.3 | 5.71 |
| βLεD (a g-)βL | 158,6 | -151.5 | 78.7 | 166.9 | 145 | -71.4 | 159.4 | 168.9 | 6.23 |
| βLεD (a g+)βL | 156.4 | -157.1 | 69.1 | -168.9 | -152.4 | 60.8 | -147.2 | 157.9 | 6.43 |
| βLδD (a g-)βL | 165.3 | 147.9 | -154.2 | -53 | -160.2 | -109 | -157.7 | 158.8 | 7.98 |
a torsion angles in degrees (°);
b Zero-point energies are included
Table 1: Torsional angles(a) for the 20 most stable HCO-Gly-L-Tyr-Gly-NH2 conformers optimized at B3LYP/6-311++G(2d,2p) level of theory and their relative energies (ΔErel) based on single-point MP2/6-311++G(2d,2p) calculation
As shown from Table 1, 6 among the 20 most stable conformers of the HCO-Gly-L-Tyr-Gly-NH2 tripeptide localized by our approach are all within the energy range of 1 kcal.mol-1. These are: βL γL)g+g+)βL, βL γL)g+g-( βL, βL βL)a g+( βL, βL βL)a g-)βL, βL γL)a g-)βL and βL γL)a g+)βL. Conducted calculations indicate βLγL)g+g+)βL as the global minimum, βL γL)g+g-)βL as the second global minimum and the third minimum higher in energy is the βL βL)a g+) βL with 0.23 and 0.29 kcal.mol-1 respectively above the global minimum. In the 6 most stable conformations, the central residue L-tyrosine, adopts either the γL or βL folds. Furthermore, calculations carried out on the studied system have also revealed that detected conformers in which the central L-Tyrosine residue adopts the D-subscript (αD, γD, δD, εD), present high relative energy values. These findings are in well agreement with the predictions of quantum computations carried out on this residue (L-Tyrosine) at DFT level of theory [15]. The structures of the 6 most stable HCO-Gly-L-Tyr-Gly-NH2 conformers are represented in Figure 4.
Conformational space exploration by using an ordinary conformational research strategy
The efficiency of the used research procedure will be tested in the following by comparing the obtained results with those derived from a commonly used ordinary hierarchical optimization strategy as detailed below.
Hierarchical optimization methodology
The 81 possible conformations of HCO-Gly-L-Tyr-Gly-NH2 tripetide model predicted by MDCA rules (Scheme 2) have been submitted first to full geometry optimization at the Hartree–Fock level of theory, using 3-21G* basis set. Resulting conformers were then optimized through RHF/6-31+G(d), and DFT/B3LYP/6-31++G(2d,2p) levels of theory respectively. The input of each conformer for the calculations at one level of theory made use of the output geometry of the corresponding structure from the previous level. Finally, obtained structures from the geometry optimization at DFT/B3LYP/6-311++G(2d,2p) level were subjected to a single point energy calculations by applying Møller–Plesset perturbation theory up to second order with 6-311++G(2d,2p) basis set including evaluation of zero-point energies (ZPEs) calculated at DFT/B3LYP/6-311++G(2d,2p). This optimization procedure is a common practice. Many previous studies have applied such strategy to calculate the PESs of molecules containing aromatic rings that present usually non-negligible dispersion attractions [4-5, 38-44].
Results
The molecular geometry optimization conducted on the 81 HCO-Gly-L-Tyr-Gly-NH2 tripeptide conformers at RHF/3-21G* level of theory revealed a total of 34 fully relaxed structures. The remaining 47 conformers migrated to one of the existing structures. Thereafter, these 34 obtained structures were submitted to full geometry optimization at RHF/6-31G+(d) and DFT/B3LYP/6-311++G(2d,2p) levels of theory, leading to 30 and 28 different conformers respectively. The energies of the 28 conformations localized at the stage of DFT/B3LYP/6-311++G(2d,2p) calculations were then evaluated by applying the MP2 theory with 6-311++G(2d,2p) basis set. Results of geometry optimizations of detected conformers including geometrical parameters and relative energies are given in Tables 2 and 3 respectively. Torsional angles and relative energies of common conformers between the developed procedure based on the use of the genetic algorithm MNC and the ordinary conformational research strategy are indicated in bold in Table 3.
| Backbone conformation (b) | Glycine (1) (βL) | Tyrosine | Glycine (2) (βL) | ΔErel (in Kcalmol-1) | |||||
|---|---|---|---|---|---|---|---|---|---|
| φ1 | ψ1 | φtyr | ψyr | χ1 | χ2 | φ2 | ψ2 | ||
| βLαL (a g+)βL | -151.3 | 145.3 | -70.8 | -39.7 | -163.2 | 73.8 | 147.4 | 146.1 | 6.74 |
| βLαD (g+ g-)βL | 154.3 | 143.4 | 52.4 | 48.2 | 50.4 | -112.3 | -145.2 | 151.9 | 8.56 |
| βLαD (g- g+)βL | 153.4 | -151.2 | 67.9 | 35.2 | -50.2 | 109.2 | -153.9 | 144.8 | 3.76 |
| βLαD (g- g-)βL | 144.2 | 144.3 | 69.1 | 33.8 | -59.3 | -82.1 | 148.2 | 149.2 | 3.86 |
| βLβL (g+g+)βL | -143.8 | -145.7 | -142.2 | 159.3 | 56.4 | 89.4 | 146.9 | -145.1 | 1.79 |
| βLβL (g+g-)βL | -153.5 | -153.4 | -144.3 | 157.2 | 56.9 | -91.5 | 145.9 | -147.5 | 1.73 |
| βLβL (a g+)βL | 146.3 | 152.5 | -147.5 | 148.1 | -159.2 | 70.9 | -144.4 | 145.1 | 0 |
| βLβL (a g-)βL | -151.2 | 146.2 | -146.5 | 147.3 | -158.1 | -106.4 | -146.5 | 151.8 | 0.11 |
| βLβL (g- g+)βL | 151.7 | -152.3 | -123.3 | 139.2 | -57.3 | 100.1 | -146.9 | 151.8 | 2.54 |
| βLβL (g- g-)βL | 153.3 | -145.9 | -130.5 | 137.6 | -64.3 | -81.7 | 144.2 | 145.5 | 2.53 |
| βLγL (g+g+)βL | -147.3 | 151.2 | -78.1 | 60.3 | 51.4 | 80.7 | 153.1 | 148.7 | 0.53 |
| βLγL (g+g-)βL | 144.3 | 152.5 | -80.8 | 58.9 | 46.9 | -110.7 | -149.3 | -145.9 | 0.84 |
| βLγL (a g+)βL | 144.3 | 146.2 | -79.4 | 72.8 | -150.1 | 86.8 | -146.9 | 146.5 | 0.57 |
| βLγL (a g-)βL | 149.1 | -147.8 | -79.4 | 73.5 | -158 | -88.5 | 151.9 | -146.3 | 0.37 |
| βLγL (g- g+)βL | 151.5 | 147 | -79.2 | 73 | -51.3 | 112.3 | -146.2 | 148.8 | 0.84 |
| βLγL (g- g-)βL | 152.5 | 146.7 | -81.6 | 70.9 | -55.4 | -70.5 | 148.4 | -153.2 | 0.89 |
| βLγD (g+g+)βL | -153.5 | 145.8 | 60.1 | -39.1 | 68.8 | 80.2 | 147.9 | 147.3 | 8.52 |
| βLγD (a g+)βL | 145.1 | 145.3 | 68.1 | -61.9 | -169.5 | 78.1 | -147.7 | 148.8 | 4.35 |
| βLγD (a g-)βL | -151.4 | -145.6 | 70.6 | -70.2 | -159.5 | -100.1 | 151.7 | 153.7 | 4.18 |
| βLγD (g- g+)βL | 149 | 145.3 | 72.3 | -59.2 | -62.4 | 109.3 | 147.4 | 151 | 2.21 |
| βLγD (g- g-)βL | -151.2 | 153 | 71.3 | -57.9 | -64.8 | -71.3 | -145.4 | 147.3 | 2.24 |
| βLδL (g+g+)βL | 148.5 | -149.4 | -130.3 | 22.5 | 57.2 | 78.2 | 146 | 149.6 | 1.28 |
| βLδL (g+g-)βL | 148.2 | -144.7 | -131.8 | 21.4 | 56.8 | -94.1 | 149 | 148.4 | 1.51 |
| βLδL (a g+)βL ➞ βL βL (a g+)βL |
146.3 | 152.5 | -147.5 | 148.1 | -159.2 | 70.9 | -144.4 | 145.1 | 0 |
| βLδL (a g-)βL ➞ βL βL (a g-)βL |
-151.2 | 146.2 | -146.5 | 147.3 | -158.1 | -106.4 | -146.5 | 151.8 | 0.11 |
| βLδL (g- g+)βL ➞ βLαL (g- g+)βL |
-149.4 | -151.2 | -77.2 | -25.3 | -57.1 | 112.2 | 151.3 | 147.2 | 3.15 |
| βLδL (g- g-)βL | 145.9 | 149.2 | -115.2 | 10.4 | -50.1 | -64.7 | 146.1 | -149.8 | 3.08 |
| βLδD (g+g+)βL | -153.4 | -145.5 | -159.3 | -27.2 | 59.2 | 90.2 | 149.7 | -153.5 | 5.44 |
| βLδD (g+g-)βL | -149.3 | 147.5 | -168.2 | -31.9 | 53.5 | -83.4 | -148.1 | -149.5 | 5.37 |
| βLδD (a g+)βL | 148.2 | 152.4 | -150.2 | -53.5 | -167.2 | 73.7 | -144.5 | -147.6 | 7.06 |
| βLεD (a g+)βL | 148.4 | 153.7 | 65.5 | -167.4 | -149.1 | 59.5 | 151.6 | 147.2 | 6.94 |
| βLεD (a g-)βL | -145 | -146.5 | 68.2 | -169.9 | -151.2 | -122.1 | 152.5 | -144.4 | 6.79 |
| βLεD (g- g+)βL ➞ βL γD (g- g+)βL |
149 | 145.3 | 72.3 | -59.2 | -62.4 | 109.3 | 147.4 | 151 | 2.21 |
| βLεD (g- g-) βL ➞ βL γD (g- g-)βL |
-151.2 | 153 | 71.3 | -57.9 | -64.8 | -71.3 | -145.4 | 147.3 | 2.24 |
a torsion angles in degrees (°);
b The observed conformational migrations at the RHF/6-31+G (d) level of theory are noted such as: input RHF/3-21G* structure ➞ output RHF/6–31+G(d) conformer
Table 2: Torsional angles(a) for backbone and side chain conformers of HCO-Gly-L-Tyr–Gly-NH2 tripeptide optimized at RHF/6-31+G(d) level of theory and their relative energies (ΔErel) calculated at the same level
| Backbone conformation (b) | Glycine (1) (βL) | Tyrosine | Glycine (2) (βL) | ΔErel (c) (Kcal.mol-1) at MP2/6-311++G (2d,2p) | |||||
|---|---|---|---|---|---|---|---|---|---|
| φ1 | ψ1 | φtyr | ψyr | χ1 | χ2 | φ2 | ψ2 | ||
| βLαL (a g+)βL ➞ βLγL (a g+) βL |
151.3 | -153.8 | -80.3 | 80.3 | -160.1 | 91.6 | -143.9 | 157.2 | 0.89 (6) |
| βLαL (g- g+)βL | -169.4 | -141.2 | -77.2 | -25.3 | -57.1 | 112.2 | 151.3 | 157.2 | 2.77 (15) |
| βLαD (g+ g+)βL | -164.3 | -153.5 | 46.3 | 43.1 | 51.3 | 76.5 | 151.5 | 152.5 | 8.48 (28) |
| βLαD (g- g+)βL | -169.2 | 153.5 | 70.2 | 23.6 | -63.5 | 107.8 | 151.2 | -156.4 | 6.24 (20) |
| βLαD (g- g-)βL | 173.4 | -158.3 | 69.3 | 25.6 | -59.7 | -78.1 | 155.6 | 151.5 | 6.53 (21) |
| βLβL (g+g+)βL | -161.2 | -155.9 | -153 | 170.6 | 60 | 79.2 | 150.6 | -153.6 | 2.13 (11) |
| βLβL (g+g-)βL | -150.2 | 157.3 | -161.3 | 171.2 | 59.1 | -90.1 | -156.1 | 152.3 | 2.83 (16) |
| βLβL (a g+)βL | 168.1 | 154.5 | -160.3 | 170.4 | -161.9 | 76.7 | -114.9 | 154.3 | 0.31 (3) |
| βLβL (a g-)βL | 164.4 | -159.3 | -160.9 | 164.6 | -159.3 | -110.6 | -144.7 | 152.7 | 0.49 (4) |
| βLβL (g- g+)βL | 161.4 | -153.3 | -121.2 | 148.3 | -60.8 | 93.4 | 153.3 | 156.4 | 6.11 (19) |
| βLβL (g- g-)βL | -163.4 | 152.5 | -124.2 | 145.3 | -61.3 | -84.2 | 144 | 157.8 | 2.71 (14) |
| βLγL (g+g+)βL | -161.2 | -150.4 | -80.2 | 58.1 | 40.3 | 79.4 | 151.2 | -150.2 | 0.00 (1) |
| βLγL (g+g-)βL | -166.4 | -156.2 | -79.8 | 57.9 | 40.7 | -102.5 | 154.5 | 154.6 | 0.26 (2) |
| βLγL (a g+)βL | 151.3 | -153.8 | -80.3 | 80.3 | -160.1 | 91.6 | -143.9 | 157.2 | 0.89 (6) |
| βLγL (a g-)βL | -169.4 | 151.9 | -80.3 | 79.2 | -161.4 | -88.9 | -145.1 | 157.9 | 0.69 (5) |
| βLγL (g- g+)βL | 169.2 | 154.3 | -81.6 | 75.6 | -52.7 | 113.1 | 153.4 | -157 | 1.12 (8) |
| βLγL (g- g-)βL | -161.9 | 150.7 | -80.8 | 73.7 | -54 | -70.1 | 153.7 | 155.7 | 1.07 (7) |
| βLγD (g+g+)βL | 163.3 | 152.3 | 53.1 | -20.2 | 65.1 | 80.6 | -157.3 | 150.6 | 7.29 (26) |
| βLγD (a g+)βL | -166.2 | -157.9 | 73.3 | -64.2 | -167.5 | 76.7 | 147.7 | 153.9 | 5.43 (18) |
| βLγD (a g-)βL | 164.9 | 159.2 | 70.3 | -68.4 | -160.1 | -93 | 150.3 | 150.9 | 5.12 (17) |
| βLγD (g- g+)βL | -163.2 | 151.9 | 72.5 | -58.4 | -59.3 | 99.3 | -145.4 | 151.5 | 1.81 (9) |
| βLγD (g- g-)βL | 160.2 | -154.7 | 71.5 | -57.9 | -58.7 | -75.6 | 150.9 | 149.4 | 1.89 (10) |
| βLδL (g+g+)βL | 164.8 | -158.7 | -125.8 | 19.2 | 54.3 | 83.5 | 149.7 | 158.8 | 2.24 (12) |
| βLδL (g+g-)βL | 169.9 | -150.6 | -123.8 | 18.4 | 55.6 | -90.1 | 160.9 | -145.7 | 2.36 (13) |
| βLδL (g- g-)βL ➞ βLβL (g- g-)βL |
-163.4 | 152.5 | -124.2 | 145.3 | -61.3 | -84.2 | 144 | 157.8 | 2.71 (14) |
| βLδD (g+g+)βL | -169.7 | 150.3 | -170.4 | -31.3 | 53.2 | 87.7 | 151.6 | 159.3 | 6.77 (23) |
| βLδD (g+g-)βL | 167.4 | 157 | -171.3 | -36.2 | 50.2 | -82.6 | 159.8 | -160.2 | 6.58 (22) |
| βLδD (a g+)βL | 163.7 | 155.6 | -160.9 | -60.6 | -168.4 | 72 | 157.2 | 153.2 | 7.80 (27) |
| βLεD (a g+)βL | 165.1 | -155.3 | 70.3 | -166.9 | -150.8 | 59.3 | -167.2 | 177.9 | 6.81 (25) |
| βLεD (a g-)βL | 169.3 | -153 | 77.5 | 167.2 | 146.2 | -70.3 | 169.4 | 178.9 | 6.78 (24) |
a Torsion angles in degrees (°);
b The observed conformational migrations at the B3LYB/ 6-311++G(2d,2p) level of theory are noted, such as: input RHF/6-31+G(d) structure ➞ output B3LYB/ 6-311++G(2d,2p) conformer;
c Zero-point energies are included. The italic numbers in parentheses indicate the relative energy ordering at MP2/ 6- 311++G(2d,2p) level of theory
Table 3: Torsional angles(a) for backbone and side chain conformers of HCO-Gly-L-Tyr–Gly-NH2 tripeptide optimized at B3LYP/6-311++G(2d,2p) level of theory and their relative energies (ΔErel) based on single-point MP2/6-311++G(2d,2p) calculations
It's worth noting that calculations conducted on the studied tripeptide using the ordinary hierarchical research strategy predicted βLγL)g+g+(βL as the global minimum, βLγL)g+g-(βL as the second global minimum and the third minimum higher in energy is the βLβL)a g( βL with 0.26 and 0.31 kcal.mol-1 respectively above the global minimum. This finding is in well accordance with predictions of the research strategy based on the genetic algorithm (Table 1 and Table 3).
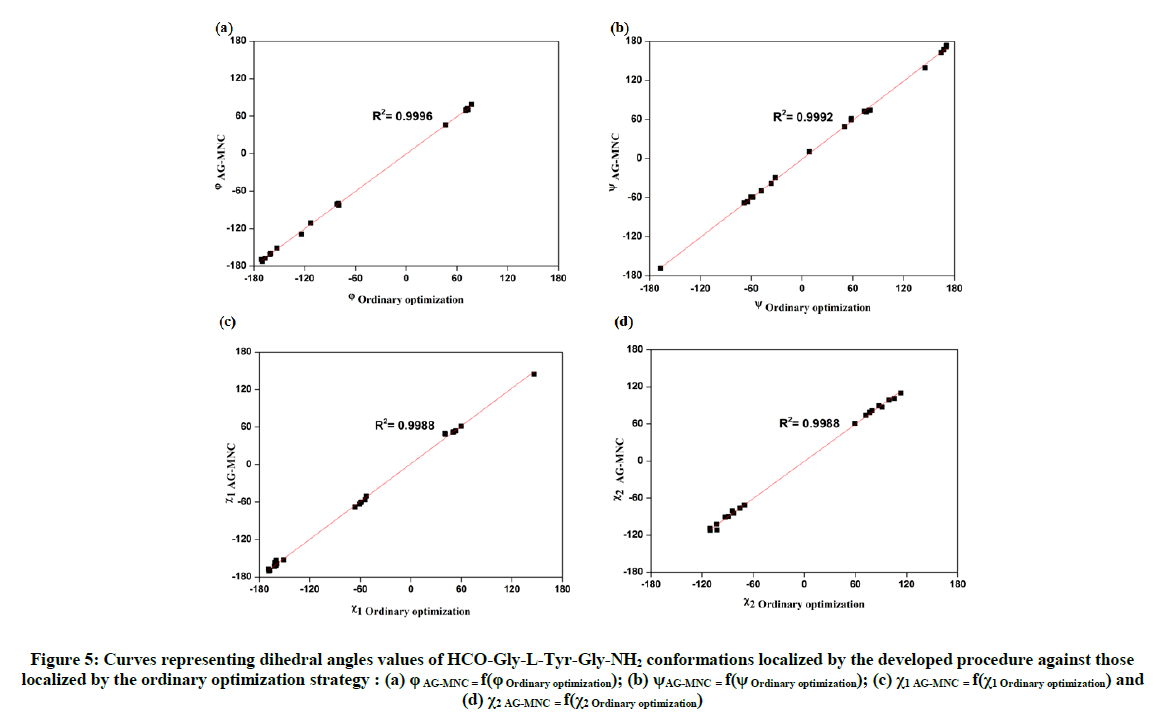
Furthermore, the 6 most stable conformers for the studied tripeptide are all within the energy range of 1 kcal.mol-1 and in the same stability order of those localized by our developed procedure. Additionally, from the results displayed in Table 1 and Table 3, one can deduce that the developed procedure based on the use of the genetic algorithm MNC combined with DFT and MP calculations was able to predict 18 conformations among the 28 one localized by the ordinary optimization strategy and in which the 11 most stables ones are in the same stability order, which reflect the higher efficiency of used method to locate most stable minima on the potential energy surface (PES) of the studied tripeptide. Dihedral angles (φTyr, ψTyr, χ1 and χ2) of the central tyrosine residue in HCO-Gly-L-Tyr-Gly-NH2 conformations localized by our procedure can be represented in function of those localized by the ordinary strategy in other to assess the concordance quality between the common conformers (Figures 5a-5d). The comparison of the dihedral angles was limited to those of the tyrosine residue, since no appreciable change was detected in the values of the dihedral angles φgly1, ψgly1, φgly2 and ψgly2, of the glycine residues, during the various stages of optimization (Tables 1 to 3).
Figure 5: Curves representing dihedral angles values of HCO-Gly-L-Tyr-Gly-NH2 conformations localized by the developed procedure against those localized by the ordinary optimization strategy : (a) φ AG-MNC = f(φ Ordinary optimization); (b) ψAG-MNC = f(ψ Ordinary optimization); (c) χ1 AG-MNC = f(χ1 Ordinary optimization) and (d) χ2 AG-MNC = f(χ2 Ordinary optimization)
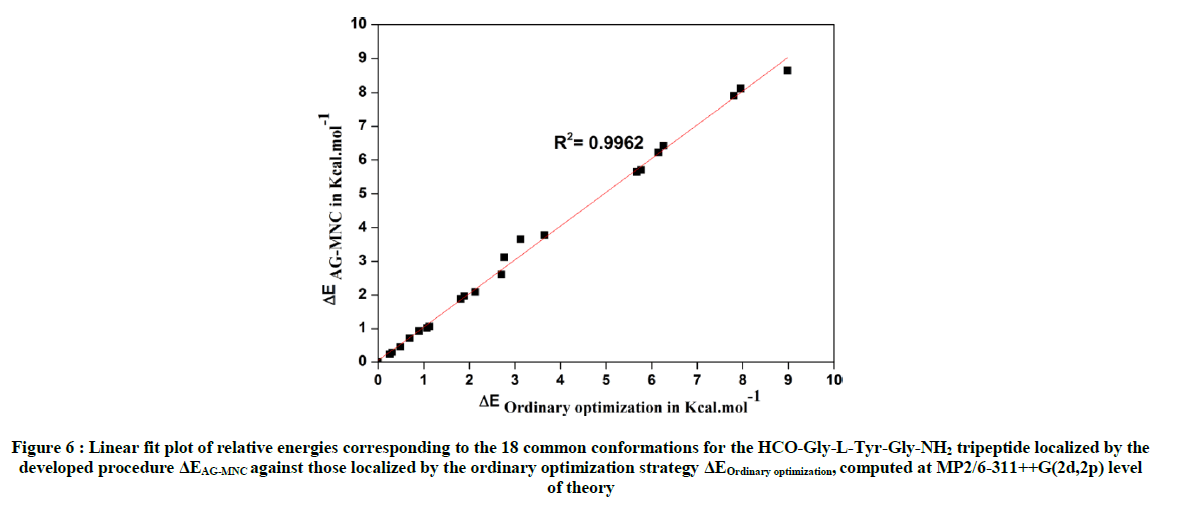
The comparison of geometries of 18 common conformations obtained either through the procedure based on the use of the genetic algorithm MNC or by the ordinary hierarchical optimization strategy, revealed nearly perfect linear adjustments with R2 values of 0.9996, 0.9992, 0.9988, and 0 9988 for the dihedral angles φTyr, ψTyr, χ1 and χ2 respectively, which reflect a good geometrical concordance quality between these conformations Otherwise, we can observe (from the spread of points in the plotted curves) that dihedral angles φ and χ2 are less ideal in terms of the population of their respective conformational space. These can be contrasted to the dihedral angles ψ and χ1, which have most of the stable conformers populating ideal states predicted by MDCA. The points representing the values of dihedral angles ψ and χ1 are intensively grouped in the probable areas predicted by MDCA (g+=60°, a=180°, g-=-60°) as shown in Figure 5b and 5c. However, the points representing both dihedral angles φ and χ2 are distributed in a random manner, which indicates the flexible nature of each of those angles (Figure 5a and 5d). Furthermore, Table 1 and Table 3 present the relative energies (ΔErel) evaluated at MP2/6-31++G(2d,2p) level of theory for the 18 HCO-Gly-L-Tyr-Gly-NH2 common conformations between both strategies used in this work. A linear fit correlation between ΔEAG-MNC (relative energies of conformations localized by the developed procedure based on the use of the genetic algorithm MNC) and ΔEOrdinary optimization (relative energies of conformations localized by the ordinary hierarchical optimization strategy) is shown in Figure 6.
Figure 6 : Linear fit plot of relative energies corresponding to the 18 common conformations for the HCO-Gly-L-Tyr-Gly-NH2 tripeptide localized by the developed procedure ΔEAG-MNC against those localized by the ordinary optimization strategy ΔEOrdinary optimization, computed at MP2/6-311++G(2d,2p) level of theory
As shown in Figure 6, the comparison of relative energies for the 18 common conformations between both strategies revealed nearly perfect linear adjustment with R2 value of 0.9962. Thus, the developed procedure based on the use of the genetic algorithm MNC was able to predict the correct energy gaps for all these common conformations.
Conclusion
In this work, a promising research, and optimization, procedure was developed in order to explore the potential energy surface of short peptide chain HCO-L-Gly-L-Tyr-Gly-NH2. This consist on the use of a genetic algorithm based on the multi niche crowding MNC technique combined with high quantum chemical calculations (at DFT and MP2 level of theory). Our calculations revealed the capacity of the developed procedure to localize the most stable minima on the PES of the studied tripeptide, in which, 11 ones are in the same stability order as expected by a commonly used ordinary hierarchical optimization strategy. Furthermore, comparison of dihedral angles which describing the spatial rearrangement of the central L-Tyrosine residue in the studied tripeptide for the 18 common conformations localized by the developed procedure with those localized by the ordinary optimization strategy geometries and their relative energies, respectively, revealed nearly perfect linear adjustments. Such procedure can offer new possibilities to explore PESs of larger-size molecules (long chain peptides) since it allows us to overcome the difficulties related to the exploration their conformational spaces, that is, to localize all probable potential equilibrium structures on their PESs, which will help in the following to better understand the macromolecules-folding problem, such as proteins, and to update the databases of biomolecular imaging and drug design softwares.
References
- F.A. Bovey, Chain Structure and Conformation of Macromolecules, Academic Press, New York, 1982.
- A. Millet, T. Korona, R. Moszynski, E. Kochanski, J. Chem. Phys., 1999, 111, 7727.
- A.D. Rabuck, G.E. Scuseria, Theor. Chem. Acc., 2000, 104, 439.
- D. Toroz, T. van Mourik, Mol. Phys., 2006, 104, 559.
- D. Toroz, T. van Mourik, Mol. Phys., 2007, 105, 209.
- S. Kirkpatrick, C.D. Gelatt, M.P. Vecchi, Science., 1983, 220, 671.
- K.A. De Jong, Machine Learning., 1988, 3, 121.
- K.A. De Jong, In: R. Manner and B. Manderick (Edi.), Are genetic algorithms function optimizers?, Elsevier, Amsterdam: North Holland, 1992, 3.
- W. Cedeno, V.R. Vemuri, T. Slezak, Evolut. Comput., 1995, 2, 321.
- A. Perczel, J.G. Angyan, M. Kajtar, W. Viviani, J.L. Rivail, J.F. Marcoccia, I.G. Csizmadia, J. Am. Chem. Soc., 1991, 113, 6256.
- P.K. Ponnuswamy, V. Sasisekharan, Biopolymers., 1971, 3, 565.
- P.N. Lewis, F.A. Momany, H.A. Scheraga, Isr. J. Chem., 1973, 11, 121.
- H.A. Baldoni, G.N. Zamarbide, R.D. Enriz, E.A. Jauregui, Ö. Farkas, A. Perczel, S.J. Salpietro, I.G. Csizmadia, J. Mol. Struct., 2000, 500, 97.
- M.F. Masman, M.A. Zamora, A.M. Rodríguez, N.G. Fidanza, N.M. Peruchena, R.D. Enriz, I.G. Csizmadia, Eur. Phys. J. D., 2002, 20, 531.
- G.A. Chass, S. Lovas, R.F. Murphy, I.G. Csizmadia, Eur. Phys. J. D., 2002, 20, 481.
- M.A. Sahai, S.S. Motiwala, G.A. Chass, E.F. Pai, B. Penke, I.G. Csizmadia, J. Mol. Struct., 2003, 666, 251.
- J.A. Bombasaro, A.M. Rodríguez, R.D. Enriz, Mol. Struct., 2005, 724, 173.
- J.A. Bombasaro, M.A. Zamora, H.A. Baldoni, R.D. Enriz, J. Phys. Chem. A., 2005, 109, 874.
- A. Mehdizadeh, G.A. Chass, Ö. Farkas, A. Perczel, L.L. Torday, A. Varro, J.G. Papp, J. Mol. Struct., 2002, 588, 187.
- I.G. Csizmadia, In: J. Beltrán, I.G. Csizmadia (Edi.), Multidimensional Theoretical Stereochemistry and Conformational Potential Energy Surface Topology, Springer, Dordrecht, 1989, 1.
- H.M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T.N. Bhat, H. Weissig, I.N. Shindyalov, P.E. Bourne, Nucleic. Acids. Res., 2000, 28, 235.
- H. Lodish, A. Berk, S.L. Zipursky, P. Matsudaira, D. Baltimore, In : W.H. Freeman (Edi.), Tumor cells and the onset of cancer, 4th (Edn.), Molecular Cell Biology, New York, 2000.
- IUPAC-IUB Commission on Biochemical Nomenclature, Biochemistry., 1970, 9, 3471.
- Ö. Farkas, A. Perczel, J.F. Marcoccia, M. Hollosi, I.G. Csizmadia, J. Mol. Struct., 1995, 331, 27.
- B. El Merbouh, M. Bourjila, R. Tijar, R.D. El Bouzaidi, A. EL Gridani, M. El Mouhtadi, J. Theor. Comput. Chem., 2014, 13, 1450067.
- A. El Guerdaoui, R. Tijar, B. El Merbouh, M. Bourjila, R.D. El Bouzaidi, A. EL Gridani, J. Mol. Graph. Model., 2017, 75, 137.
- A. El Guerdaoui, B. El Merbouh, R. Tijar, M. Bourjila, R.D. El Bouzaidi, A. EL Gridani, Comptes Rendus Chimie., 2017, 20, 500.
- J.J.P. Stewart, J. Comput. Chem., 1988, 10, 209.
- D.E. Goldberg, K. Deb, J.H. Clark, Compl. Syst., 1992, 6, 333.
- A.D. Becke, Phys. Rev. A., 1998, 38, 3098.
- A.D. Becke, J. Chem. Phys., 1993, 98, 5648.
- L. F. Holroyd, T. van Mourik, Chem. Phys. Lett., 2007, 442, 42.
- F.B. van Duijneveldt, G.C.M. van Duijneveldt-van de Rijdt, J.H. van Lenthe, Chem. Rev., 1994, 94, 1873.
- R. Crespo-Otero, L.A. Monteroa, J. Chem. Phys., 2015, 123, 1.
- B. Paizs, S. Suhai, J. Comput. Chem., 1998, 19, 575.
- T. Van mourik, A.K. Wilson, K.A. Peterson, D.E. Woon, T.H. Dunning, Adv. Quantum. Chem., 1998, 31, 105.
- M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, G. Scalman, V. Barone, B. Mennucci, G.A. Petersson, H. Takatsuki, M. Caricato, X. Li, H.P. Hratchian, A.F. Izmaylov, J. Bloino, G. Zheng, J.L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J.A. Montgomery Jr., J.E. Peralta, F. Ogliaro, M. Bearpark, J.J. Heyd, E. Brothers, K.N. Kudin, V.N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J.C. Burant, S.S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J.M. Millam, M. Klene, J.E. Knox, J.B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R.E. Stratmann, O. Yazyev, A.J. Austin, R. Cammi, C. Pomelli, J.W. Ochterski, R.L. Martin, K. Morokuma, V.G. Zakrzewski, G.A. Voth, P. Salvador, J.J. Dannenberg, S. Dapprich, A.D. Daniels, O. Farkas, J.B. Foresman, J.V. Ortiz, J. Cioslowski, and D.J. Fox, Gaussian 09, Gaussian Inc., Wallingford CT, 2009.
- W.Chin, J.P. Dognon, F. Piuzzi, B. Tardivel, I. Dimicoli, M. Mons, J. Am. Chem. Soc., 2005, 127, 707.
- W. Chin, J.P. Dognon, C. Canuel, F. Piuzzi, I. Dimicoli, M. Mons, I. Compagnon, G. von Helden, G. Meijer, J. Chem. Phys., 2005, 122, 1.
- L.C. Snoek, R.T. Kroemer, M.R. Hockridge, J.P. Simons, Phys. Chem. Chem. Phys., 2001, 3, 1819.
- L.C. Snoek, T. van Mourik, and J.P. Simons, Molec. Phys., 2003, 101, 1239.
- M. Gerhards, C. Unterberg, A. Gerlach, A. Jansen, Phys. Chem. Chem. Phys., 2004, 6, 2682.
- P. Çarçabal, L.C. Snoek, T. van Mourik, Molec. Phys., 2005, 103, 1633.
- T.D. Vaden, T.S.J.A. de Boer, N.A. MacLeod, E.M. Marzluff, J.P. Simons, L.C. Snoek, Phys. Chem. Chem. Phys., 2007, 9, 2549.