Phonon Study of Mg₂Sio₄ by using [VTBFS] Model

Srivastava UC^*

Deptartment of Physics, Amity Institute of applied Sciences, Amity University, Noida, U.P, 201301, India

*Corresponding Author:

Srivastava UC
Deptartment of Physics
Amity Institute of applied Sciences
Amity University
Noida, U.P, 201301, India

Abstract

In present manuscript author use lattice dynamical model ‘van der Waals three-body force shell model’ [VTBFSM] theoretical study of Mg₂SiO₄. The structural and physical data of simple oxides and potential was reported empirically by previous other different models for Mg₂SiO₄. The present model [VTBFS] is a advance model over previous used lattice models and it simply derived by fitting to the spectroscopic data with inclusion of (VW) and (TB) interaction in the frame work of (IRSM) ion polarizable rigid shell model. Density functional theory (DFT) was used to optimize the crystal structure of Mg₂SiO₄ thereafter studied about the thermal properties and (DOS) at the temperature 500 K. However, a considerable improvement on computational results has observed, which successfully predicted the properties of Mg₂SiO₄ and their aggregates validity with experimental results.

Keywords

Phonon, Thermal properties, Density of state, Van der Waals Interaction.

Introduction

Studies of forsterite Mg₂SiO₄ has been reported by (DF) theory, which depict its structural properties at various phases [1,2]. The pioneer work of Kellerman [3] for alkali halides and rock salt crystals has been devoted a considerable attention for theoretical and experimental study [4-7]. The lattice dynamic is the best methods for the complete study of structural properties of material. In the present work origin of (VWI) potential is important component and the correlations of the motion of electron in different atoms and inclusion of effects of TBI and VWI in frame work of RSM. The free-electron approximations and Hietler London theory is employed in same frame work which shows a significance advances over previous lattice models. The aim of mineralogical research is to analysed existence and the stability of minerals and also compositional conditions under given pressure and temperature. The quantum mechanical studies have much complexity so it has less utility. But the study of crystal behaviour is simpler by atomistic approach. By use of this approach we can predict the defect and physical properties of crystals. The lattice dynamic approach is important in study of geophysics because it underlies our understanding of the influence of temperature on physical properties and thermal expansion that drives convention of mantle and core.

Materials and Methods

Theory

In past decade, first principles lattice dynamics with the (QHA) quasi harmonic approximation has been applied to predict vibrational and thermal properties of mantle minerals. On study of vibrational spectral properties we can understand the micro and macro behaviour of minerals and apply same for study of thermal properties. The theory of thermal conductivity also drives from concepts of phonons; the theory of lattice dynamics is well developed and illustrating between microscopic and macroscopic properties. In transition zone thermal, structural and elastic properties are affected the dynamic of Mg₂SiO₄. The orthorhombic structure of will not change until 1890°C exothermic phase transition, which lead to a discontinuous increase in the density of the Earth's-mantle and continues to be a material of considerable theoretical and experimental interest. The unit cell has 4 formulas (28 atoms), 84 vibrational modes among which 3 acoustic and 81 optical modes are at each q point in the Brillouin zone. Many high-pressure measurements of thermodynamic properties [8-10] are available today. Meanwhile, empirical potential based previous lattice dynamic calculation [11] on forsterite are limited to the usage of semi-classical potentials and molecular dynamic calculation [12] and recently pseudopotential calculations based on first principles [13], has been successfully applied to predict the structural and elastic properties of Mg₂SiO₄. The availability of experimental result has motivated to author for the study of thermal properties of Mg₂SiO₄. The Primitive and Crystallographic unit Shell Structures are illustrate in Figure 1.

Figure 1: (a) Primitive Structural view of Mg₂SiO₄, (b) Crystallographic view of Mg₂SiO₄

Lattice parameter, atomic coordinates and cell parameters are experimentally reported [14] for forsterite as a=4.7503 Å, b=10.187 Å, and c=5.9771 Å. The irreducible representation of forsterite lattice at the Brillouin Zone center is as in equation.

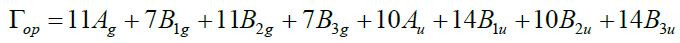(1)

Where, 11A_g+7B_1g+11B_2g+7B_3g are Raman active; 14B_1u+10B_2u+14B_3u are infrared active; 10 A_u are inactive. Three acoustic modes are B1u+B2u+B3u. For complete rigorously derived and exactly evaluated harmonic dynamical behaviour of the forsterite Mg₂SiO₄ has given in the framework of RSM [15-17],which is known [VTBFS] model. The general formalism and relevant expression of present model is given by

Φ= Φ^C+Φ^R+Φ^TBI+Φ^VWI (2)

Where, Coulomb interaction potential Φ^C is given as

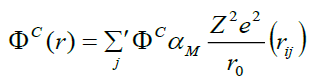
Where α_m is the Modelung constant the secular equation for it given as [15-17]:

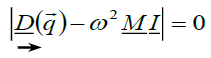(3)

If we consider only the second neighbour dipole-dipole van der Waals interaction energy, then it is expressed [18] as:

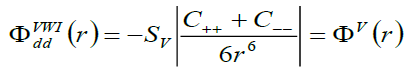(4)

Where, S_v is lattice sum and the constants C₊₊ and C_-- are the VdW coefficients corresponding to the positive-positive and negative-negative ion pairs, respectively.

Thermodynamically properties of Mg₂SiO₄

The geophysical significance of lattice vibrations is not only for their connection to elasticity but also it governs most thermal properties of earth material with their magnitude. The total vibrational energy of a crystal is the sum over all the phonon modes in the Brillouin zone (BZ) and mechanism of soft phonon mode, which is the major cause of phase transformations of Mg₂SiO₄ [19] shows its importance in present study. In the QHA formulation, the Helmholtz free energy can be expressed as:

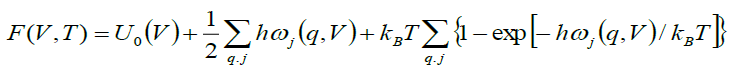(5)

where the first term is the internal energy, the second is zero point motion energy, and the third is the vibrational energy contribution, where ωj represents phonons with normal mode q. The thermal properties of forsterite Mg₂SiO₄ compared with the computed phonon spectra at the temperature 500 K. The theoretical calculated thermal properties of Mg₂SiO₄ reported by using the VASP software [20-22] coupled with Phonon [23] and compared with experimental or others’ simulation results [24,25]. Specific heat capacity at constant volume (Cv) is calculated using equation (7).

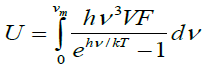(6)

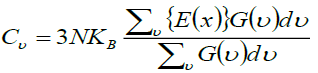and (7)

Where, Einstein function is difiend as 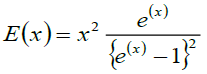and = Total number of frequencies interval, E(v) is the Einstein function and R the gas constant. According to thermodynamic, the equilibrium of a solid at a temperature T is determined by the minimum value of the free energy.

F=E-TS (8)

The equation for entropy (ΔS) of a system is given as

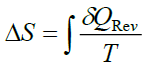(9)

Density of States

To determine phonon density of states for each polarization i.e., the number of states per interval of energy at each energy level available to be occupied is given by

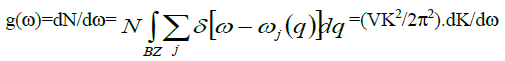(10)

N = (L/2π)³(4πK³/3), K is wave vector and L³=V. where N as a normalization constant such that 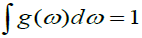and 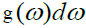are eigen states in the frequency interval 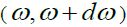to the total number

Computations

The pressure effect, electronic, structurer and vibrational properties has calculated out by use of DFT Phonon and [VTBFS] model in present paper. Calculation has conducted after the optimization of geometry of the crystal. The different thermal property curve at temperature range 0- 500 K has shown in Figures 2-6. The property of Mg₂SiO₄ has investigated by using the first principles method. The validity of calculated lattice parameters and thermodynamical curve by use of available experimental data has shown in figure.

Figure 2: Internal Energy curve of Mg₂SiO₄

Figure 3: Free Energy of Mg₂SiO₄

Figure 4: Entropy curve of Mg₂SiO₄

Figure 5: Heat Capacity curve of Mg₂SiO₄

Figure 6: Density of states curve of Mg₂SiO₄

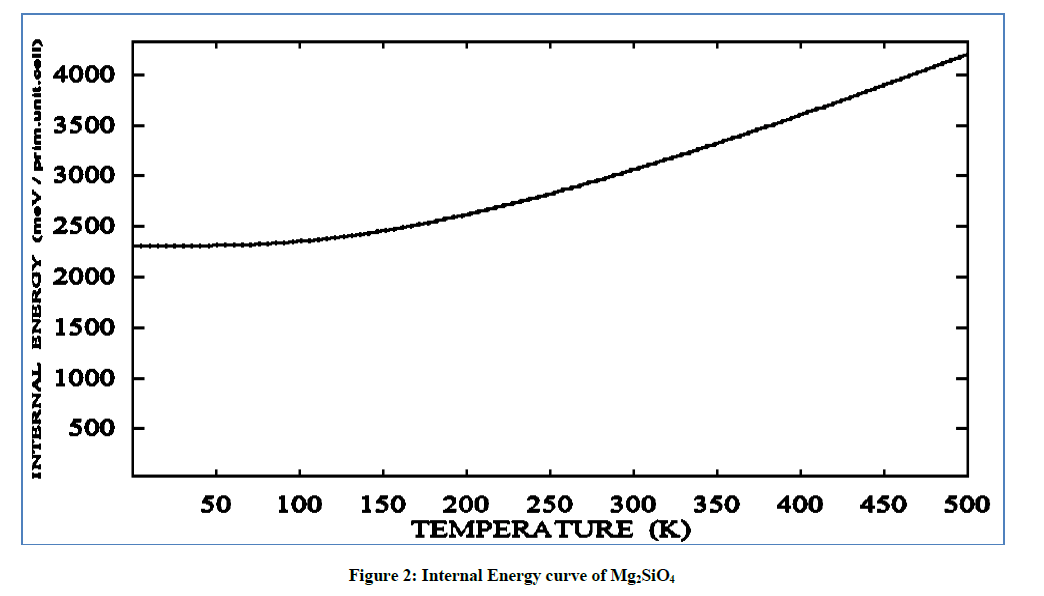
The internal energy value is started from 2300 (meV/prim. unit. cell) at 0 K and 4000 (meV/prim. unit. cell) at the temperature of 500 K at higher temperature value the energy value has varies from 2000-2400 (meV/prim. unit. cell) attended from 500 K. On increasing the temperature the internal energy is increased sharply i.e. discontinuous increase in the density of the Earth's -mantle.

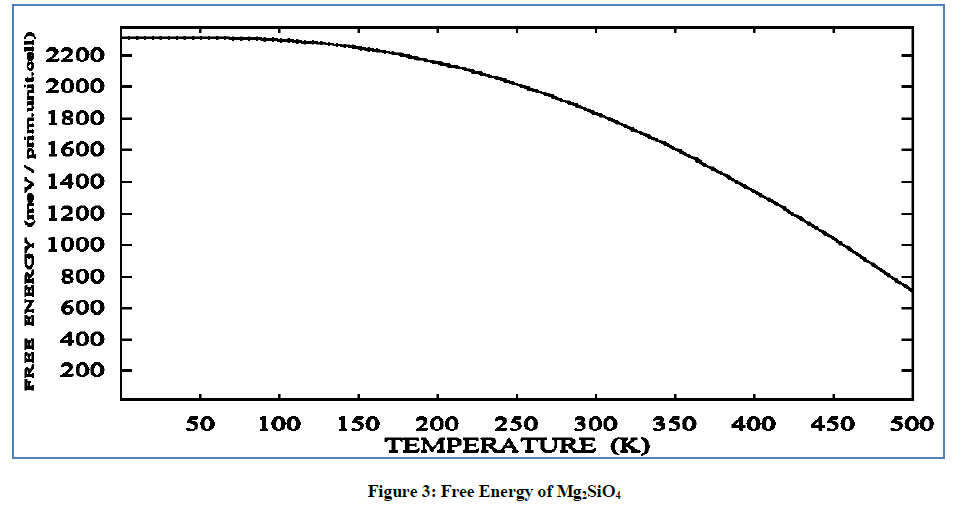
On raising the temperature the free energy value of Mg₂SiO₄ is continuously decreases on increasing the temperature. In Figure 3, on the 500 K free energy value decreasing continuously at 2400 (meV/pri. unit. cell) till 750 (meV/prim. unit. cell) attaining at the temperature 500 K. So on increasing temperature the free energy of crystal tends to high –ve (maximum decrement) value.

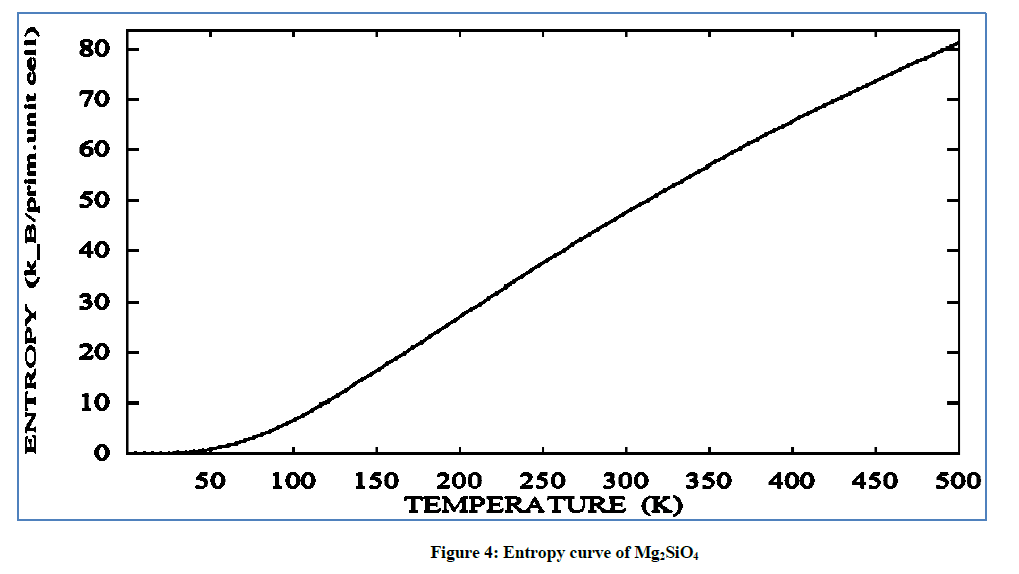
In plot of entropy versus temperature for Mg₂SiO₄ has shown in Figure 4. The curve spread over a wide range of temperature for entropy value is continuously increasing upto 80 (K-B/Prim. unit. cell) on the temperature of 500 K. On increasing the temperature value entropy of the forsterite, shifted towards zero and then sharply increase the entropy value. Sharp increase and abrupt change is noted in entropy for 0-80 towards higher temperature, so entropy is more ordered then at the temperature of 500 K.

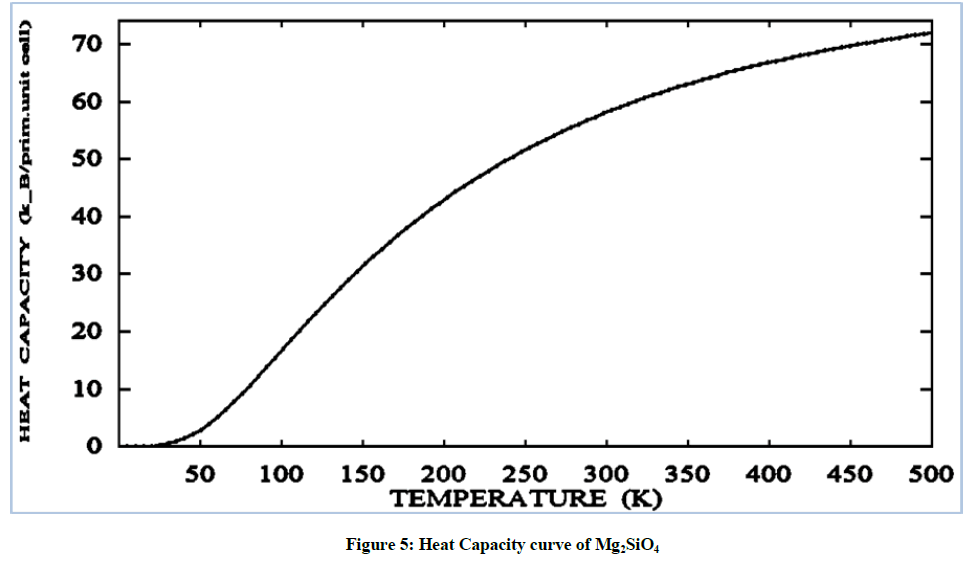
The heat capacity of increases continuously on variation of temperature value from 0 to 70 (k-B/prim. unit. cell) at the temperature range of 500 K. The exponentially increment in specific heat value curve has been observed. At 500 K the heat capacity of forsterite smoothly increases but on other higher value of temperature heat capacity increases very small and then remains constant for further increases in temperature.

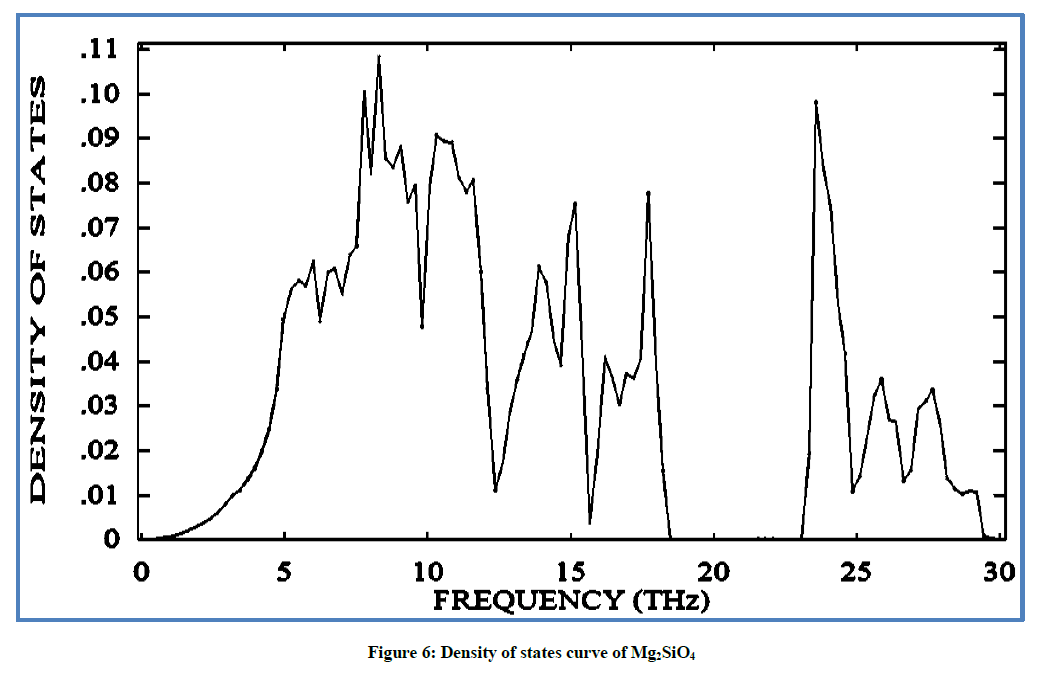
The theoretical study of (DOS) for Mg₂SiO₄ is used as a reference and their finding with the experimental observations is a qualitative agreement. The DOS curve with frequency value is reported in Figure 6. At lower frequency 7.5 (THz) the peak gain the maximum value and local density of states (LDOS) also available at frequency of 18.5 (THz). The more or less occupied states are available above the frequency 23 (THz). Distortion in peaks can be seen again at 24 (THz)-30 (THz). The illustrated thermodynamic properties obtained confirmed the characteristics of Mg₂SiO₄.

Results

To sum up, we can say that present model [VTBFS] is adequately capable of describing the crystal dynamics and thermal study of forsterite Mg₂SiO₄ in essential contributions of VWI and TBI. In the present study despite the lower symmetry of Mg₂SiO₄ and the uncertainty as to the exact nature of the distortion of the lower–temperature structure. A tremendous change in the nature of slope has been observed at temperature 500 K. The present study shows significant properties and the validity of the present model at 1ower temperature side but at the higher temperature side slight disagreement may be ascribed to the non-inclusion of the harmonic interactions in used present model, which it may be inferred that the incorporation of van der Waals interactions is essential. The phonon study of forsterite Mg₂SiO₄ theoretically reported is well agreed with experimental result [26,27]. Our research group and others have been used successfully the present model for the study of alkali halides, semiconductor and chalcogenide materials [28-42].

References

1. M. Houssa, V.V. Afanaśev, A. Stesmans, M.M. Heyns, Appl. Phys. Lett., 2000, 77, 1885.
2. S.J. Wang, Appl. Phys. Lett., 2001, 78, 1604.
3. E.W. Kellerman, Phil. Trans. Roy. Soc., London, 1940, A238, 513.
4. P.O. Lowdin, Ark. Mat. Astr. Fys., Sweden, 1947, 35A, 30.
5. S.O. Lundqvist, Ark. Fys., Sweden, 1952, 6, 25.
6. S.O. Lundqvist, Ark. Fys., Sweden, 1955, 9, 435.
7. S.O. Lundqvist, Ark. Fys., Sweden, 1957, 12, 263.
8. M. Akaogi, E. Ito, A. Navrotsky, J. Geophys. Res., 1989, 15(94), 671-685.
9. Y. Meng, Y. Fei, D.J. Weidner, G.D. Gwanmesia, J. Hu, Phys. Chem. Miner., 1994, 21, 407-412.
10. T. Katsura, J. Geophys. Res., 2004, 109, B12209.
11. G.D. Price, S.C. Parker, M. Leslieand, Phys. Chem. Miner., 1987, 15, 181-190.
12. M. Matsui, Phys. Earth Planet. Inter., 1999, 116, 9-18.
13. P. Piekarz, P.T. Jochym, K. Parlinski, J. Lazewski, J. Chem. Phys., 2002, 117, 3340-3344.
14. Takeuchi, Y.T. Yamanaka, N. Haga, M. Hirano, I. Sunagawa (Edi.), Terra Scientific Publishing, Tokyo, 1984, 191-231.
15. M.P. Verma, R.K. Singh, Phys. Stat. Sol., 1969, 33, 769(1969);
16. M.P. Verma, R.K. Singh, Phys. Stat. Sol., 1969, 36, 335.
17. M.P. Verma, R.K. Singh, Phys. Stat. Sol., 1970, 38, 851.
18. J.E. Potts, C.T. Walker, Phys. Rev. B., 1973, 6, 2456.
19. O. Sugino, R. Car, Phys. Rev. Lett., 1995, 74, 1823-1826.
20. G. Kresse, J. Non-Crystalline Solids., 1995, 19, 222-229.
21. P.F. Manicone, P.R. Iommetti, L. Raffaelli, J. Dentist., 2007, 35, 819-826.
22. D. Vanderbilt, Phys. Rev. B., Condensed matter, 1990, 41, 7892-7895.
23. A. Togo, F. Oba, I. Tanaka, Phys. Rev. B, 2008, 78, 134106.
24. N.P. de Koker, L. Stixrude, B.B. Karki, Geochim. et Cosmochim. Acta., 2008, 72, 1427-1441.
25. G.D. Price, Minerological Magazine, 1987, 51, 157-70.
26. G.B. Martin, F.J. Spera, M. S. Ghiorso, D. Nevins, Am. Mineralogist., 2009, 94, 693-703.
27. C.W.F.T. Pistorious, J.B. Clark, Phy. Rev., 1968, 3, 173.
28. R.K. Ram, S.S. Kushwaha, J. Phys. Soc. Japan., 1985, 54, 617 (1985).
29. M.S. Kushwaha, S.S. Kushwaha, Canad. J. Phys., 1980, 58, 351.
30. R.K. Singh, P. Khare, Phys. Stat. Sol. (b)., 1981, 103, 337.
31. R.K. Singh, P. Khare, J. Phys. Soc. Japan, 1982, 51, 141.
32. R.K. Singh, N.V.K. Prabhakar, Phys. Stat. Sol. (b)., 1988, 111, 146.
33. K.S. Upadhyaya, M. Yadav, G.K. Upadhyaya, Phys. Status Solidi, 2002,1129, B229.
34. S.K. Tiwari, K.S Upadhyaya, Phys. Scr., 2009, 80, 65603-65606).
35. U.C. Srivastava, R.S. Pandey, K.S. Upadhyaya, Int. J. Phys. Sci., 2010, 5(7), 972-977.
36. U.C. Srivastava, K.S. Upadhyaya, Optoelect. Adv. Materials., Rapid Comm. (OAM-RC), 2010, 9(4), 1336-1341.
37. U.C. Srivastava, K.S. Upadhyaya, Phys. Rev. Res. Int., 2011, 1(1), (16-28).
38. U.C. Srivastava, British J. Appl. Phys. Technol., 2012, 2(1), 35-47.
39. U.C. Srivastava, Optoelectro. Adv. Mater. Rapid Commun.,2013, 7, 698-701.
40. U.C. Srivastava, Optoelectro. Adv. Mater. Rapid Commun., 2013, 9-10.
41. J.P. Dubey, R.K. Tiwari, K.S. Upadhyaya, P.K. Pandey, Turk. J. Phys., 2015, 39(242-253).
42. U.C. Srivastava, Int. J. Modern Phys. B., 2016, 30, 1750020-1750028.