Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 3
Thermo-physical Studies on Molecular Interactions in Liquid Binaries of Diethyl Malonate and Isomeric Xylenes at Various Temperatures
Venkateswararao VNSR1, Satyanarayana GR2, Beebi SK3 and Rambabu C1*
1Department of Chemistry, Acharya Nagarjuna University, Guntur-522510, Andrapradesh, India
2Department of Chemistry, Sir. C.R. Reddy PG College, Eluru-534007, Andrapradesh, India
3Department of Chemistry, Y.V.N.R. Govt. Degree College, Kaikaluru-521333, Andrapradesh, India
- *Corresponding Author:
- Rambabu C
Department of Chemistry
Acharya Nagarjuna University
Guntur-522510, Andrapradesh, India
Abstract
Densities and viscosities of binary liquid mixtures of diethyl malonate with isomeric xylenes were reported at (303.15, 308.15, 313.15 and 318.15 K). From the experimental data, deviation in Viscosity (Δη) and excess Gibbs free energy of activation of Viscous flow (ΔG*E) were evaluated. The deviations in viscosity and excess Gibbs free energy of activation of viscous flow were correlated with Redlich-Kister polynomial equation. Viscosity theories like Grunberg-Nissan, Katti-Chaudhri, Heric-Brewer, Hind et al. and McAllister four body models have been applied to correlate the viscosity of binary mixtures.
Keywords
Density, Viscosity, Gibbs free energy, Molecular interaction
Introduction
Density and viscosity play a vital role in analyzing the theoretical and physical properties of binary liquids. The experimental results of these properties of the binary liquids attracted the attention of large number of engineering and chemical industries [1]. The viscosity of binary liquids is a tremendous tool in many chemical applications such as molecular structure, mass, liquid stream, heat transfer and capillary electrophoresis [2]. Moreover, the investigation of excess thermodynamics and transport properties for binary mixture gives essential data concerning the deeper understanding of the molecular liquid structure and intermolecular interactions [3]. Xylenes are habitually utilized as octane enhancer in vehicles [4]. They likewise have different applications in printing, elastic, petrochemical ventures and leather industries. Diethyl Malonate (DEM) is a diethyl ester of malonic acid.
In this study, viscosities and densities are measured at four temperatures (303.15, 308.15, 313.15 and 318.15) K for binary mixtures of Diethyl Malonate (DEM) with o-Xylene (OX), m-xylene (MX) and p-Xylene (PX). Deviation in Viscosity (Δη) and excess Gibbs free energy of activation of Viscous flow (ΔG*E) have been computed from Density (ρ) and Viscosity (η) information to understand the nature of forces working between them. Semi-empirical viscosity models, for example, Grunberg and Nissan [5], Katti and Chaudhri [6], Heric and Brewer [7], Hind et al., [8] and McAllister [9] four body models are utilized to compare the investigational results with the theoretical viscosities.
Experimental Section
Materials and methods
Diethyl malonate and isomeric xylenes provided from Merck were purified as depicted in the literature [10,11]. The unadulterated chemicals were stored over activated molecular sieves to decrease water content before utilize. All the binary liquid mixtures are prepared gravimetrically utilizing an electronic balance (Shimadzu AY 120) with an uncertainty of ± 1 × 10-7 kg and stored in sealed shut containers. The uncertainty on mole fraction is evaluated to be 1 × 10-4. It is guaranteed that the mixtures are appropriately mixed and the estimation of the required parameters was done within one day of preparation. The densities (ρ) of unadulterated liquids and their mixtures are determined utilizing a 10-5 m3 double-arm Pycnometer and the values from triplicate replication at every temperature are reproducible within 2 × 10-1 kg.m-3 and the uncertainty in the estimation of density is observed to be 2 parts in 104 parts. The reproducibility in mole fractions was within ± 0.0002. Temperature control for the estimation of viscosity and density is accomplished by utilizing a microprocessor assisted circulating water bath regulated to ± 0.01 K, utilizing a corresponding temperature controller. Satisfactory precautionary measures were taken to limit evaporation losses during the genuine estimations. Exploratory estimations of density and viscosity at 303.15-318.15 K with those detailed in the literature [12-15,4] are provided in Table 1.
| 303.15 K | 308.15 K | 313.15 K | 318.15 K | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ (10-3 kg m-3) | η (m Pa s) | ρ (10-3 kg m-3) | η (m Pa s) | ρ (10-3 kg m-3) | η (m Pa s) | ρ (10-3 kg m-3) | η (m Pa s) | ||||||||
| Expt. | Lit. | Expt. | Lit. | Expt. | Lit. | Expt. | Lit. | Expt. | Lit. | Expt. | Lit. | Expt. | Lit. | Expt. | Lit. |
| 1.0443 | 1.0443a | 1.73 | 1.732b | 1.0385 | 1.0387a | 1.602 | 1.602b | 1.0335 | 1.0336a | 1.456 | 1.458b | 1.0313 | 1.4244 | 1.425b | |
| 0.8704 | 0.8707c | 0.7061 | 0.7051c | 0.8695 | 0.8694c | 0.665 | 0.6652c | 0.8678 | 0.8677c | 0.6226 | 0.6211c | 0.8658 | 0.8659c | 0.569 | 0.5691c |
| 0.8555 | 0.8557c | 0.555 | 0.5530d | 0.8485 | 0.8487c | 0.5224 | 0.523d | 0.8455 | 0.8458c | 0.493 | 0.493d | 0.8403 | 0.8405c | 0.4686 | 0.468d |
| 0.8529 | 0.8529e | 0.577 | 0.5782c | 0.8468 | 0.8460c | 0.551 | 0.5501c | 0.8428 | 0.8430c | 0.505 | 0.5065c | 0.837 | 0.8369c | 0.492 | 0.4912c |
since a=12, b=13, c=14, d=15, e=16
Table 1: Comparison of density (ρ) and Viscosity (η) of the pure liquids with literature data
Theoretical considerations
The viscosity deviations (Δη) were calculated utilizing:
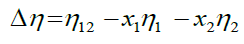 (1)
(1)
Where, η12 is the viscosity of the binary mixture, x1, x2 and η1, η1 are the mole fraction and the viscosities of unadulterated segments 1 and 2, respectively. The dynamic viscosities of the liquid mixtures have been computed utilizing observational relations given by Grunberg-Nissan, Katti-Chaudari, Heric-Brewer, Hind et al. and McAllister four body models. Grunberg and Nissan [5] proposed the following equation for the estimation of viscosity of liquid mixtures:
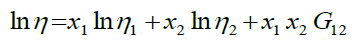 (2)
(2)
Where, G12 is an interaction parameter, which is an element of viscosity of segment liquids 1 and 2 and temperature. Katti and Chaudhri [6] equation for the dynamic viscosity of the liquid mixture is:
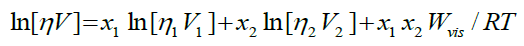 (3)
(3)
Where, Wvis is an interaction term, Heric and Brewer [7] determined the following equation to calculate the viscosity of the binary liquid mixtures:
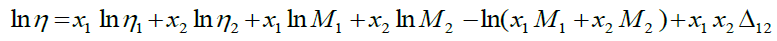 (4)
(4)
Where, Δ12 is the association term and other symbols have their typical importance. The expression to determine the viscosity of the binary liquid mixtures proposed by Hind et al. [8] is given by:
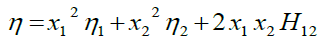 (5)
(5)
Where, H12 is an association term, McAllister [9] four body interaction model was generally used to correlate kinematic viscosity (v) information. The 2 parameter McAllister equation based on Eyring’s theory of absolute reaction rates, considered collaborations of both like and unlike molecules by a two dimensional four body model. The four body model was characterized by the connection:
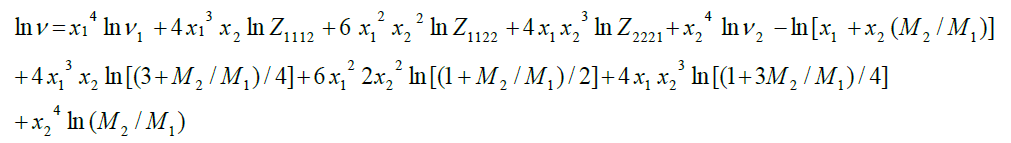 (6)
(6)
Where, Z1112, Z1122 and Z2221 are model parameters and Mi and Vi are the molecular mass and kinematic viscosity of pure component i. To perform a numerical comparison of the correlating capability of above equations, we have calculated the standard percentage deviation (σ %) utilizing the connection:
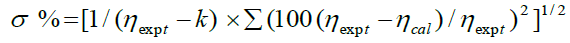 (7)
(7)
Where, k speaks to the quantity of numerical coefficients in the respective equation. These parameters assessed by a non-linear regression analysis based on a least-squares strategy and given their standard percentage deviation (σ %) in Table 2
| T/K | G12 | σ | Wvis/RT | σ | Δ12 | σ | H12 | σ | Z1112 | Z1122 | Z2221 | σ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diethyl malonate + o-xylene | ||||||||||||
| 303.15 | 1.5107 | 0.0638 | 1.4823 | 0.064 | 1.5957 | 0.065 | 1.8831 | 0.0178 | 1.7387 | 1.7718 | 1.4772 | 0.0045 |
| 308.15 | 1.4092 | 0.0522 | 1.3756 | 0.0523 | 1.4943 | 0.0533 | 1.7068 | 0.0175 | 1.5858 | 1.6464 | 1.327 | 0.0062 |
| 313.15 | 1.3491 | 0.0437 | 1.312 | 0.0439 | 1.4343 | 0.0447 | 1.5497 | 0.0163 | 1.433 | 1.5215 | 1.1926 | 0.0058 |
| 318.15 | 1.2889 | 0.0371 | 1.2477 | 0.0372 | 1.3741 | 0.0381 | 1.4214 | 0.0189 | 1.3447 | 1.4864 | 1.0561 | 0.0034 |
| Diethyl malonate + m-xylene | ||||||||||||
| 303.15 | 1.8886 | 0.0921 | 1.8215 | 0.0916 | 1.9731 | 0.0932 | 1.8147 | 0.0172 | 1.7369 | 1.6312 | 1.4696 | 0.005 |
| 308.15 | 1.7753 | 0.0761 | 1.7041 | 0.0754 | 1.86 | 0.0771 | 1.6418 | 0.0165 | 1.5816 | 1.5156 | 1.3125 | 0.0057 |
| 313.15 | 1.6888 | 0.0627 | 1.614 | 0.0621 | 1.7735 | 0.0636 | 1.4897 | 0.0158 | 1.4256 | 1.4121 | 1.1678 | 0.0057 |
| 318.15 | 1.5748 | 0.0509 | 1.4945 | 0.0504 | 1.6597 | 0.0519 | 1.3796 | 0.0188 | 1.3406 | 1.4054 | 1.036 | 0.003 |
| Diethyl malonate + p-xylene | ||||||||||||
| 303.15 | 1.8996 | 0.0932 | 1.8235 | 0.0925 | 1.9841 | 0.0943 | 1.8712 | 0.0173 | 1.763 | 1.6646 | 1.519 | 0.0048 |
| 308.15 | 1.7834 | 0.0773 | 1.7059 | 0.0766 | 1.868 | 0.0784 | 1.7081 | 0.0169 | 1.6089 | 1.5587 | 1.3698 | 0.0056 |
| 313.15 | 1.6945 | 0.0629 | 1.616 | 0.0623 | 1.7793 | 0.0639 | 1.518 | 0.0158 | 1.4389 | 1.43 | 1.1904 | 0.0056 |
| 318.15 | 1.5821 | 0.0517 | 1.4988 | 0.0512 | 1.667 | 0.0527 | 1.4291 | 0.0187 | 1.3614 | 1.4385 | 1.0769 | 0.003 |
Table 2: Interaction Parameters and the corresponding standard deviations (σ) for the binary mixtures of diethyl malonate and studied isomeric xylenes at various temperatures
On the premise of the theories of absolute reaction rates [16], the excess Gibbs free energy of activation of viscous flow was computed by utilizing the connection:
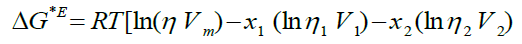 (8)
(8)
Where, η and Vm are the dynamic viscosity and molar volume of the mixture. η1, η2 and V1, V2 are viscosity and molar volume of pure components 1 and 2 individually. R is the real gas constant and T is the absolute temperature. The composition dependence of Δη and ΔG*E(YEcal) for each mixture are fitted to Redlich-Kister polynomial equation [17]:
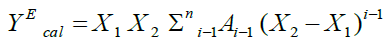 (9)
(9)
The coefficients of Ai-1 in the above equation alongside the standard deviation σ (YE) have been ascertained. These coefficients are the adjustable parameters to get best - fit values of YEcal. The standard deviations σ of YEcal were computed by utilizing the connection:
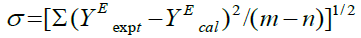 (10)
(10)
Where, m is the quantity of experimental data points and n is the number of coefficients considered and YEexpt, YEcal are the values of experimental and calculated property (Δη and ΔG*E) separately.
Diethyl malonate is an aprotic solvent which has a solid inclination to pull electron in carbon – oxygen bond towards itself. It has a dynamic methylene gathering and shows dipole-dipole interactions in the unadulterated state. The investigational values of viscosity and computed estimations of deviation in viscosity and excess Gibbs free energy of activation of viscous flow for three binary mixtures (DEM+OX/MX/PX) at various temperatures (303.15, 308.15, 313.15 and 318.15) K are displayed in Table 3. Excess/deviation quantities are correlated by Redlich- Kister polynomial as an element of temperature. The fitting coefficients Ai-1 for all the three binary mixtures are recorded in Table 4 along with their standard deviation σ (root mean square deviation).
| 303.15 K | 308.15 K | 313.15 K | 318.15 K | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | η | Δη | ΔG*E | η | Δη | ΔG*E | η | Δη | ΔG*E | η | Δη | ΔG*E |
| Diethyl malonate + o-xylene | ||||||||||||
| 0.0000 | 0.706 | 0 | 0 | 0.665 | 0 | 0 | 0.623 | 0 | 0 | 0.569 | 0 | 0 |
| 0.0812 | 0.875 | 0.086 | 352.37 | 0.808 | 0.067 | 309.93 | 0.752 | 0.061 | 303.83 | 0.684 | 0.046 | 282.21 |
| 0.1658 | 1.051 | 0.175 | 618.62 | 0.971 | 0.151 | 584.6 | 0.889 | 0.128 | 546.14 | 0.812 | 0.101 | 523.5 |
| 0.2542 | 1.236 | 0.27 | 824.02 | 1.14 | 0.237 | 792.16 | 1.046 | 0.211 | 768.99 | 0.953 | 0.167 | 726.62 |
| 0.3465 | 1.387 | 0.326 | 901.74 | 1.275 | 0.285 | 866.4 | 1.164 | 0.252 | 838.05 | 1.076 | 0.211 | 817.98 |
| 0.443 | 1.509 | 0.349 | 894.81 | 1.384 | 0.304 | 857.61 | 1.266 | 0.274 | 841.71 | 1.186 | 0.238 | 839.49 |
| 0.544 | 1.615 | 0.352 | 838.28 | 1.479 | 0.304 | 800.66 | 1.35 | 0.274 | 786.3 | 1.274 | 0.24 | 784.32 |
| 0.6498 | 1.696 | 0.325 | 724.34 | 1.555 | 0.281 | 692.46 | 1.414 | 0.25 | 675.16 | 1.345 | 0.22 | 673.44 |
| 0.7608 | 1.722 | 0.237 | 515.06 | 1.586 | 0.208 | 496.9 | 1.441 | 0.184 | 483.34 | 1.377 | 0.157 | 471.21 |
| 0.8774 | 1.724 | 0.12 | 260.02 | 1.591 | 0.104 | 248.83 | 1.447 | 0.093 | 243.98 | 1.395 | 0.076 | 231.03 |
| 1.0000 | 1.73 | 0 | 0 | 1.602 | 0 | 0 | 1.456 | 0 | 0 | 1.424 | 0 | 0 |
| Diethyl malonate + m-xylene | ||||||||||||
| 0.0000 | 0.555 | 0 | 0 | 0.522 | 0 | 0 | 0.493 | 0 | 0 | 0.469 | 0 | 0 |
| 0.0825 | 0.74 | 0.088 | 472.99 | 0.68 | 0.069 | 423.02 | 0.635 | 0.063 | 407.75 | 0.596 | 0.048 | 371.23 |
| 0.1683 | 0.93 | 0.177 | 793.77 | 0.858 | 0.154 | 762.6 | 0.785 | 0.13 | 707.73 | 0.733 | 0.103 | 655 |
| 0.2575 | 1.13 | 0.272 | 1021.78 | 1.039 | 0.239 | 989.05 | 0.954 | 0.213 | 956.34 | 0.884 | 0.169 | 879.72 |
| 0.3504 | 1.295 | 0.328 | 1093.74 | 1.187 | 0.287 | 1057.89 | 1.084 | 0.254 | 1021.68 | 1.017 | 0.213 | 971.64 |
| 0.4473 | 1.433 | 0.352 | 1068.98 | 1.311 | 0.306 | 1031.7 | 1.199 | 0.276 | 1008.74 | 1.137 | 0.241 | 979.29 |
| 0.5483 | 1.555 | 0.356 | 986.74 | 1.422 | 0.308 | 950.82 | 1.297 | 0.276 | 927.99 | 1.238 | 0.245 | 907.81 |
| 0.6537 | 1.651 | 0.328 | 839.19 | 1.511 | 0.283 | 807.27 | 1.375 | 0.252 | 786.17 | 1.317 | 0.224 | 766 |
| 0.764 | 1.692 | 0.239 | 590.45 | 1.557 | 0.21 | 573.44 | 1.415 | 0.186 | 557.6 | 1.358 | 0.159 | 531.52 |
| 0.8793 | 1.71 | 0.122 | 297.23 | 1.578 | 0.106 | 287.36 | 1.435 | 0.095 | 280.83 | 1.387 | 0.078 | 261.8 |
| 1.0000 | 1.73 | 0 | 0 | 1.602 | 0 | 0 | 1.456 | 0 | 0 | 1.424 | 0 | 0 |
| Diethyl malonate + p-xylene | ||||||||||||
| 0.0000 | 0.577 | 0 | 0 | 0.551 | 0 | 0 | 0.505 | 0 | 0 | 0.492 | 0 | 0 |
| 0.0827 | 0.768 | 0.096 | 473.89 | 0.716 | 0.078 | 425.56 | 0.65 | 0.066 | 409.14 | 0.624 | 0.055 | 374.79 |
| 0.1687 | 0.964 | 0.193 | 797.81 | 0.899 | 0.171 | 763.36 | 0.802 | 0.137 | 708.82 | 0.764 | 0.115 | 656.99 |
| 0.2581 | 1.166 | 0.291 | 1022.1 | 1.084 | 0.262 | 990.36 | 0.973 | 0.223 | 957.19 | 0.918 | 0.185 | 882.3 |
| 0.3511 | 1.332 | 0.35 | 1094.5 | 1.232 | 0.312 | 1057.98 | 1.103 | 0.264 | 1021.82 | 1.051 | 0.232 | 972.78 |
| 0.448 | 1.469 | 0.375 | 1070.01 | 1.354 | 0.332 | 1032.1 | 1.218 | 0.287 | 1010.11 | 1.17 | 0.26 | 981.11 |
| 0.549 | 1.588 | 0.378 | 988.2 | 1.461 | 0.333 | 951.95 | 1.314 | 0.287 | 929.02 | 1.268 | 0.264 | 909.89 |
| 0.6544 | 1.678 | 0.346 | 839.45 | 1.543 | 0.304 | 808.05 | 1.389 | 0.262 | 787.44 | 1.341 | 0.239 | 766.61 |
| 0.7645 | 1.712 | 0.254 | 591.76 | 1.58 | 0.226 | 574.2 | 1.425 | 0.193 | 557.96 | 1.375 | 0.17 | 531.68 |
| 0.8796 | 1.721 | 0.13 | 298.1 | 1.59 | 0.115 | 287.39 | 1.441 | 0.1 | 282.18 | 1.397 | 0.085 | 263.46 |
| 1.0000 | 1.73 | 0 | 0 | 1.602 | 0 | 0 | 1.456 | 0 | 0 | 1.424 | 0 | 0 |
Table 3: Viscosity, η (m Pa s), deviation in viscosity, Δη (m Pa s) and excess Gibbs free energy of activation of viscous flow, ΔG*E (Jmol-1) for the binary mixtures of diethyl malonate and isomeric xylenes at various temperatures
| Property | Temp (K) | A0 | A1 | A2 | A3 | A4 | σ |
|---|---|---|---|---|---|---|---|
| Diethyl malonate + o-xylene | |||||||
| Δη (m Pa s) | 303.15 | 1.4137 | -0.0236 | 0.2506 | 0.2247 | -1.1151 | 0.0077 |
| 308.15 | 1.225 | 0.0259 | 0.3229 | 0.0528 | -1.2314 | 0.0057 | |
| 313.15 | 1.1038 | 0.0407 | 0.1659 | 0.0183 | -0.9088 | 0.0069 | |
| 318.15 | 0.9739 | -0.0597 | -0.2052 | 0.1073 | -0.46 | 0.0042 | |
| ΔG*E (Jmol-1) | 303.15 | 3465.29 | 1253.547 | 1370.517 | 471.6292 | -2093.47 | 13.6779 |
| 308.15 | 3307.13 | 1293.438 | 1648.547 | 46.7655 | -2884.83 | 12.0507 | |
| 313.15 | 3249.124 | 1273.93 | 1323.686 | 0.4554 | -2381.6 | 17.9204 | |
| 318.15 | 3270.533 | 1110.997 | 395.3116 | 61.7989 | -1486.61 | 10.1959 | |
| Diethyl malonate + m-xylene | |||||||
| Δη (m Pa s) | 303.15 | 1.4268 | -0.0539 | 0.2302 | 0.2311 | -1.0576 | 0.0078 |
| 308.15 | 1.2339 | 0.0043 | 0.3129 | 0.0502 | -1.179 | 0.0054 | |
| 313.15 | 1.1127 | 0.0198 | 0.1582 | 0.0199 | -0.8612 | 0.0069 | |
| 318.15 | 0.9873 | -0.0972 | -0.2063 | 0.1445 | -0.4366 | 0.0045 | |
| ΔG*E (Jmol-1) | 303.15 | 4120.746 | 1740.811 | 1707.524 | 758.8105 | -1968.94 | 15.2292 |
| 308.15 | 3960.967 | 1800.282 | 2018.676 | 212.267 | -2892.19 | 12.0754 | |
| 313.15 | 3876.974 | 1750.618 | 1695.694 | 129.119 | -2486.33 | 19.1586 | |
| 318.15 | 3799.511 | 1470.171 | 587.1788 | 233.1599 | -1372.62 | 11.5816 | |
| Diethyl malonate + p-xylene | |||||||
| Δη (m Pa s) | 303.15 | 1.517 | -0.028 | 0.2076 | 0.2096 | -1.0199 | 0.0068 |
| 308.15 | 1.3352 | 0.0363 | 0.3368 | 0.0291 | -1.2142 | 0.0055 | |
| 313.15 | 1.1558 | 0.0257 | 0.2 | 0.0019 | -0.9231 | 0.0074 | |
| 318.15 | 1.0615 | -0.0761 | -0.2174 | 0.1295 | -0.4061 | 0.0046 | |
| ΔG*E (Jmol-1) | 303.15 | 4127.674 | 1735.429 | 1671.676 | 742.463 | -1909.63 | 13.834 |
| 308.15 | 3965.943 | 1787.299 | 2015.433 | 238.7783 | -2868.52 | 12.3211 | |
| 313.15 | 3885.783 | 1739.739 | 1669.768 | 124.6681 | -2434.53 | 19.3599 | |
| 318.15 | 3808.254 | 1469.713 | 567.8503 | 234.8453 | -1293.3 | 12.192 | |
Table 4: Redlich-Kister coefficients Ai-1 and corresponding standard deviations (σ) computed for excess/deviation properties of the binary mixtures of diethyl Malonate + isomeric xylenes (o-xylene, m-xylene, p-xylene) at various temperatures
Viscosity deviation
The value and magnitude of Δη depend on molecular size and shape of the components in addition to intermolecular forces. It is observed (Table 3) that deviation in viscosity is positive for all the systems (DEM+OX/MX/PX) and at all the temperatures. The absolute value of viscosity deviation of (DEM+OX/MX/PX) systems builds directly and scopes to a greatest incentive at x1 ~ 0.5440 for (DEM+OX), x1 ~ 0.5483 for (DEM+MX), x1 ~ 0.5490 for (DEM+PX), after which step by step diminishes until pure condition of diethyl malonate is arrived. By and large, negative estimations of Δη demonstrate the presence of dispersion forces or mutual loss of specific interactions in molecules working in the systems and positive estimations of deviation in viscosity show solid particular collaborations [18-21]. As indicated by Kauzmann and Eyring [22], the viscosity of a mixture unequivocally relies upon the entropy of mixture, which is connected with the structure of the liquid. Vogel and Weiss [23] clarified that mixtures with solid communications between various molecules and negative deviations from Raoult’s law display positive viscosity deviations while for mixtures with positive deviations of Raoult’s law and without particular connections, the viscosity deviations are negative.
The less positive Δη esteems for diethyl malonate + o-xylene system show that associations are weaker over diethyl malonate + m-xylene and diethyl malonate + p-xylene systems [24], which recommends that the position of –CH3 groups on the aromatic ring assumes a generous part in choosing the extent Δη and, thus, the order of collaboration between the component molecules of the mixtures. The stereo normality of methyl groups in o-xylene is such that the steric repulsion is more. So that the Δη esteems for o-xylene are observed to be lower than the m-xylene and p-xylene. On account of p-xylene, the two methyl groups disperse similarly the π-electron cloud on the benzene ring, in this manner the charge transfer complex development between diethyl malonate and p-xylene brings about higher positive Δη esteems. The diethylmalonate + p-xylene mixtures are described by more positive Δη esteems than the mixtures of diethylmalonate + m-xylene and diethylmalonate + o-xylene, regardless of the way that p-xylene very nearly a zero dipole moment and thus dipole-induced dipole associations are not anticipated. One conceivable explanation behind this could be that p-xylene molecule is planar and flat type and can shape closer and parallel n-π complexes with slightest steric hindrance. The Δη esteems diminish with increment of temperature for all the three systems. This might be clarified as takes after: viscosity is principally the force exhibited by one layer of molecules on the neighboring layer of molecules. With the temperature rise, the cluster breakage causes weak associations and hence less force is exhibited on the adjacent layers which bring about the bringing down of deviation in viscosities. In this manner, the molecular communication follows the order:
DEM+OX<DEM+MX<DEM+PX
Excess Gibbs free energy of activation of viscous flow
The excess Gibbs free energy of activation of viscous flow like viscosity deviation can be utilized to detect molecular communications [25]. The excess Gibbs free energy of activation of viscous flow is positive for (DEM+OX/MX/PX) systems over the whole composition range and at all the temperatures. This shows the nearness of appealing strengths between the constituent molecules in the binary mixtures under examination. ΔG*E values diminishes with temperature ascend for all the three systems. This shows the debilitating of intermolecular communications at hoisted temperatures [26] and this is might be credited to detachment of related molecules through breakage of clusters both in the mixtures and immaculate solvents.
Analysing viscosity of fluid mixtures by semi observational models
In this article, we utilize the conditions of Grunberg-Nissan, Katti-Chaudhri, Heric-Brewer, Hind et al. furthermore, McAllister four body models to connect the viscosities of binary mixtures of (DEM+OX/MX/PX). Experimental and computed estimations of viscosity (η) for the binary mixtures of (DEM+OX/MX/PX) at 303.15 K are displayed in Table 5. Interaction (adjustable) Parameters computed from equations 2-6 and the relating standard deviations (σ) for all the binary mixtures are appeared in Table 2. An examination of information in Table 5 demonstrates that all the observational relations gave a sensible fit, but the viscosity values computed utilizing McAllister 4 body models are in great concurrence with the experimental values. Examination of information in Table 2 demonstrates that the estimations of interaction parameters (d) computed from various viscosity theories are positive for the systems: (DEM+OX/MX/PX) at the four distinct temperatures.
| 303.15 K | ||||||
|---|---|---|---|---|---|---|
| x1 | η Expt | η GN | η KC | η HB | η H | η Mc |
| Diethyl malonate + o-xylene | ||||||
| 0.0000 | 0.706 | 0.706 | 0.706 | 0.706 | 0.706 | 0.706 |
| 0.0812 | 0.875 | 0.85 | 0.85 | 0.849 | 0.888 | 0.873 |
| 0.1658 | 1.051 | 1.009 | 1.009 | 1.008 | 1.06 | 1.036 |
| 0.2542 | 1.236 | 1.181 | 1.181 | 1.18 | 1.218 | 1.188 |
| 0.3465 | 1.387 | 1.356 | 1.357 | 1.355 | 1.362 | 1.324 |
| 0.443 | 1.509 | 1.525 | 1.525 | 1.524 | 1.488 | 1.441 |
| 0.544 | 1.615 | 1.672 | 1.673 | 1.673 | 1.593 | 1.54 |
| 0.6498 | 1.696 | 1.783 | 1.783 | 1.784 | 1.674 | 1.624 |
| 0.7608 | 1.722 | 1.838 | 1.838 | 1.84 | 1.727 | 1.69 |
| 0.8774 | 1.724 | 1.823 | 1.824 | 1.825 | 1.748 | 1.731 |
| 1.0000 | 1.73 | 1.73 | 1.73 | 1.73 | 1.73 | 1.73 |
| Diethyl malonate + m-xylene | ||||||
| 0.0000 | 0.555 | 0.555 | 0.555 | 0.555 | 0.555 | 0.555 |
| 0.0825 | 0.74 | 0.703 | 0.704 | 0.703 | 0.754 | 0.738 |
| 0.1683 | 0.93 | 0.875 | 0.876 | 0.874 | 0.941 | 0.933 |
| 0.2575 | 1.13 | 1.067 | 1.067 | 1.066 | 1.115 | 1.123 |
| 0.3504 | 1.295 | 1.271 | 1.27 | 1.27 | 1.273 | 1.297 |
| 0.4473 | 1.433 | 1.472 | 1.471 | 1.472 | 1.413 | 1.443 |
| 0.5483 | 1.555 | 1.653 | 1.651 | 1.653 | 1.532 | 1.556 |
| 0.6537 | 1.651 | 1.79 | 1.787 | 1.791 | 1.627 | 1.638 |
| 0.764 | 1.692 | 1.86 | 1.859 | 1.862 | 1.695 | 1.691 |
| 0.8793 | 1.71 | 1.843 | 1.844 | 1.845 | 1.731 | 1.72 |
| 1.0000 | 1.73 | 1.73 | 1.73 | 1.73 | 1.73 | 1.73 |
| Diethyl malonate + p-xylene | ||||||
| 0.0000 | 0.577 | 0.577 | 0.577 | 0.577 | 0.577 | 0.577 |
| 0.0827 | 0.768 | 0.73 | 0.731 | 0.729 | 0.781 | 0.767 |
| 0.1687 | 0.964 | 0.906 | 0.907 | 0.905 | 0.973 | 0.966 |
| 0.2581 | 1.166 | 1.102 | 1.102 | 1.101 | 1.149 | 1.16 |
| 0.3511 | 1.332 | 1.308 | 1.307 | 1.307 | 1.309 | 1.334 |
| 0.448 | 1.469 | 1.51 | 1.508 | 1.509 | 1.449 | 1.479 |
| 0.549 | 1.588 | 1.688 | 1.685 | 1.688 | 1.565 | 1.589 |
| 0.6544 | 1.678 | 1.819 | 1.817 | 1.821 | 1.656 | 1.665 |
| 0.7645 | 1.712 | 1.881 | 1.88 | 1.883 | 1.717 | 1.711 |
| 0.8796 | 1.721 | 1.854 | 1.855 | 1.855 | 1.743 | 1.731 |
| 1.0000 | 1.73 | 1.73 | 1.73 | 1.73 | 1.73 | 1.73 |
Table 5: Experimental and computed estimations of viscosity, η (m Pa s) for the binary mixtures of diethyl malonate + o-xylene, diethyl malonate + m-xylene, diethyl malonate + p-xylene at 303.15 K
As indicated by Fort and Moore [27], G12 is dealt with as a precise estimation to discover the quality of association between the components. On the off chance that G12 is positive, at that point the system shows property of solid connection, on the off chance that it is negative; it is having the property of feeble communication. So also, Nigam and Mahl [28] inferred that: (i) If Δη > 0, G12 > 0 and the magnitudes of the above are large then solid particular cooperation’s would happen; (ii) If Δη < 0, G12 > 0 then feeble associations would exist; (iii) If Δη < 0, G12 < 0 and the extents of both are huge then the dispersion force would be predominant. In the present binary systems (DEM+OX/MX/PX), G12 esteems in the Table 5 are positive and viscosity deviation is positive (Δη > 0) consequently one could state that solid particular cooperation’s would display in the present binary mixtures.
Conclusion
From the estimations of viscosity and density, deviation in viscosity and excess Gibbs free energy of activation of viscous flow are computed. The exploratory estimations of viscosity were associated with the semi exact relations of viscosity like Grunberg-Nissan, Katti-Chaudhri, Heric-Brewer, Hind et al., and McAllister four body models. Among the entire relations McAllister four body model gave great concurrence with the experimental values. From the watched positive estimations of Δη, ΔG*E and G12 interaction parameter, it is presumed that strong molecular interactions are available among the concentrated binary mixtures.
References
- K. Lal, N. Tripathi, G.P. Dubey, J. Chem. Eng. Data., 2000, 45, 961.
- V. Shkolnikov, G.S. Daniel, P.F. David, G.S. Juan, Sensors and Actuators B., 2010, 150, 556.
- J.H. Yang, L.Y. Dai, X.Z. Wang, Y.Q. Chen, J. Chem. Eng. Data., 2009, 54, 2332.
- M.V. Rathnam, S. Mohite, M.S.S. Kumar, Ind. J. Chem. Tech., 2008, 15, 409.
- L. Grunberg, A.H. Nissan, Nature., 1949, 164, 799.
- P.K. Katti, M.M. Chaudhri, J. Chem. Eng. Data., 1964, 9, 442.
- E.L. Heric, J.G. Brewer, J. Chem. Eng. Data., 1967, 12, 574.
- R.K. Hind, E. McLaughlin, A.R. Ubbelohde, Trans. Faraday Soc., 1960, 56, 328.
- R.A. McAllister, AIChE Journal., 1960, 6, 427.
- J.A. Riddick, W.B. Bunger, T.K. Sakano, Organic Solvents, Physical Properties and Methods of Purification, Techniques of Chemistry, 4th Edn., Wiley Interscience, New York, USA, 1986, 2.
- B.S. Furniss, A.J. Hannaford, P.W.G. Smith, A.R. Tatchell, Vogel’s Textbook of Practical Organic Chemistry, 5th Edn., Wiley, New York, USA, 1989.
- M.V. Rathnam, M. Sudhir, M.S. Kumar, J. Serb. Chem. Soc., 2011, 76, 1.
- C.H. Udayalakshmi, K.A.K. Raj Kumar, V.N.S.R Venkateswararao, P.B. Sandhyasri, G.R. Satyanarayana, C. Rambabu, Der Pharma Chemica., 2016, 8, 209.
- K. Narendra, Ch. Srinivasu, P. Narayana Murthy, J. Appl. Sci., 2012, 12, 136.
- A. Jouyban, S.H. Maljaei, Sh. Soltanpour, M.A.A. Fakhree, J. Mol. Liq., 2011, 162, 50.
- S. Glasstone, K.J. Laidler, H. Erying, The Theory of Rate Process, McGraw- Hill, New York, USA, 1941.
- O. Redilch, A.T. Kister, Ind. Eng. Chem., 1948, 40, 345.
- M.R. Islam, S.K. Quadri, Thermochimica Acta., 1987, 115, 335.
- K. Tiwari, C. Patra, V. Chakravortty, Acoustics Letters., 1995, 19, 53.
- M. Kondaiah, K. Sreekanth, D.S. Kumar, S.M. Nayeem, D.K. Rao, J. Therm. Anal. Calorim., 2014, 118, 475.
- S.C. Bhatia, R. Bhatia, G.P. Dubey, J. Mol. Liq., 2009, 144, 163.
- W. Kauzmann, H. Eyring, J. Am. Chem. Soc., 1940, 62, 3113.
- H. Vogel, A. Weiss, Ber. Bunsenges. Phys. Chem., 1982, 86, 193.
- M.V. Rathnam, M. Sudhir, J. Chem. Eng. Data., 2005, 50, 325.
- A. Mariano, M. Postigo, Fluid Phase Equilib., 2006, 239, 146.
- G.R. Satyanarayana, D. Bala Karuna Kumar, K. Sujatha, G. Lakshmanarao, C. Rambabu, J. Mol. Liq.,2016, 216, 526.
- R.J. Fort, W.R. Moore, Trans. Faraday Soc., 1966, 62, 1112.
- R.K. Nigam, B.S. Mahl, Ind. J. Chem., 1971, 9, 1255.